2023.06.25.(일)

6장. 블럭 암호 운용

정보보안 일반 - 블럭 암호 운영모드 CBC, ECB, CTR, CFB

블럭 암호 운용 방식 (block cipher modes of operation)

암호학에서는 블록 암호 운용 방식은 하나의 키에서 블록 암호를 반복적으로 안전하게 이용하게 하는 절차를 말한다.
블록 암호는 특정 길이의 블럭 단위로 동작하기 때문에, 가변 길이 데이터를 암호화하기 위해서는 먼저 이들을 단위 블록들로 나누어야 하며, 그 블록들을 어떻게 암호화할지 정해야 하는데, 이때 블록들의 암호화 방식을 운용 방식 이라 부른다.

초기화 벡터 IV (Initialization vector)

첫 블록을 암호화할 때 사용되는 값 (1단계 앞의 암호문 블록이 존재하지 않으므로 대신하는 비트 블록을 의미) => CBC 모드에서 사용
암호화 때마다 다른 랜덤 비트열을 이용하는 것이 보통

패딩 (padding)

마지막 블록이 블록의 길이와 항상 딱 맞아 떨어지지 않기 때문에, 부족한 길이 만큼을 ‘0’으로 채우거나 임의의 비트들로 채워 넣는 것을 의미

종류

  • ECB 모드 (electronic codebook, 전자코드북)
    운용 방식 중 가장 간단한 구조를 가지며, 암호화하려는 메세지를 여러 블록으로 나누어 각각 암호화하는 방식으로 되어 있다.

ECB

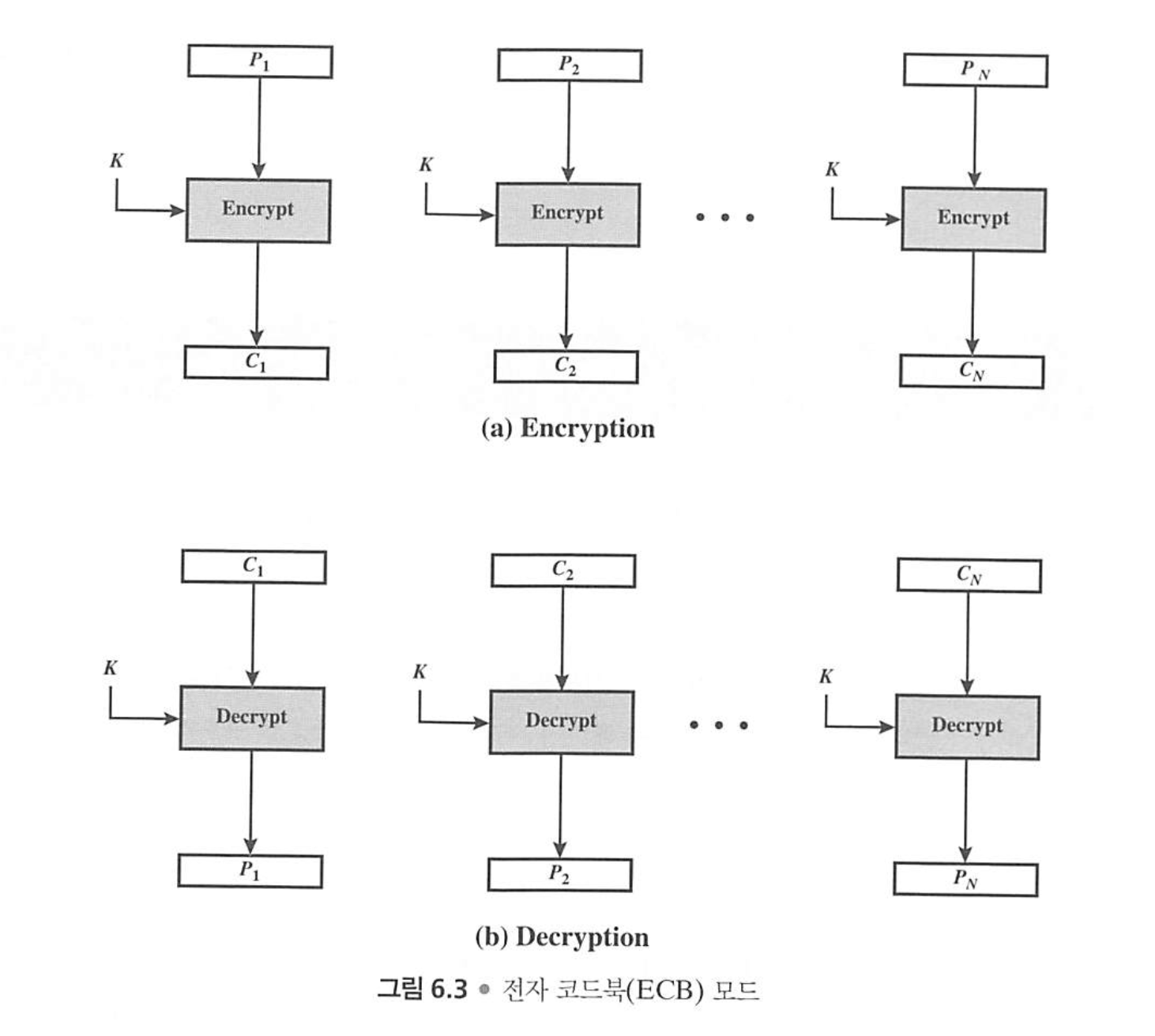
전자 코드북 (ECB) 는 모든 블록이 같은 암호화 키를 사용하기 때문에 보안에 취약하다.
만약 암호화 메세지를 여러 부분으로 나누었을 때 두 블럭이 같은 값을 가진다면, 암호화한 값 역시 같다.
=> 반복공격 (Brute-Force Attack, Dictionary Attack) 에 취약

  • CBC 모드 (cipher block chaining, 암호 블록 체인 방식)
    각 블록은 암호화되기 전에 이전 블록의 암호화 결과와 XOR 되며, 첫 블록의 경우 초기화 벡터 (IV) 가 사용된다.
    초기화 벡터가 같은 경우 출력 결과가 항상 같기 때문에, 매 암호화마다 다른 초기화 벡터를 사용해야 한다.

CBC

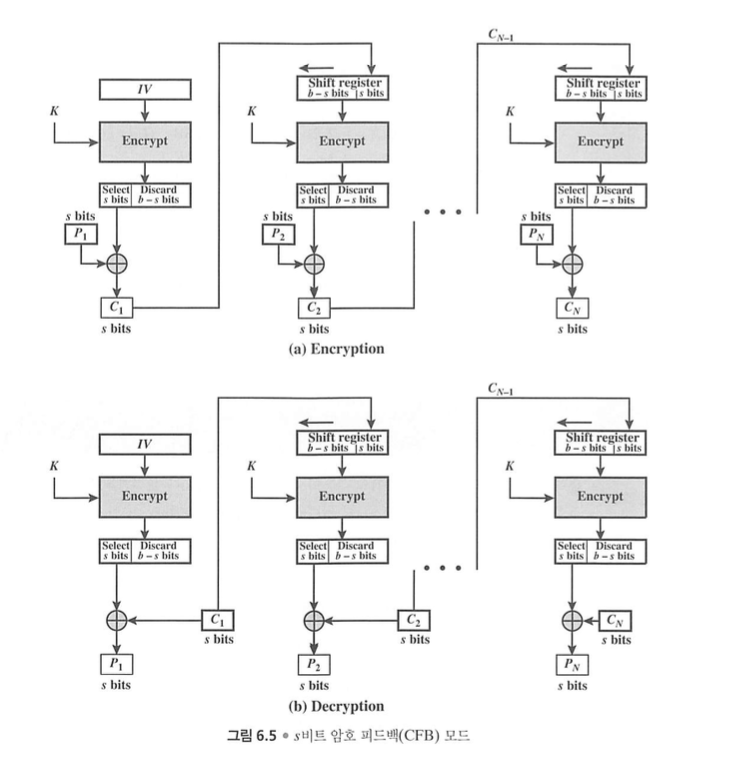
  • CFB 모드 (cipher feedback, 암호 피드백)
    CBC의 변형으로, 블록 암호를 자기 동기 스트림 암호로 변환한다.

CBC

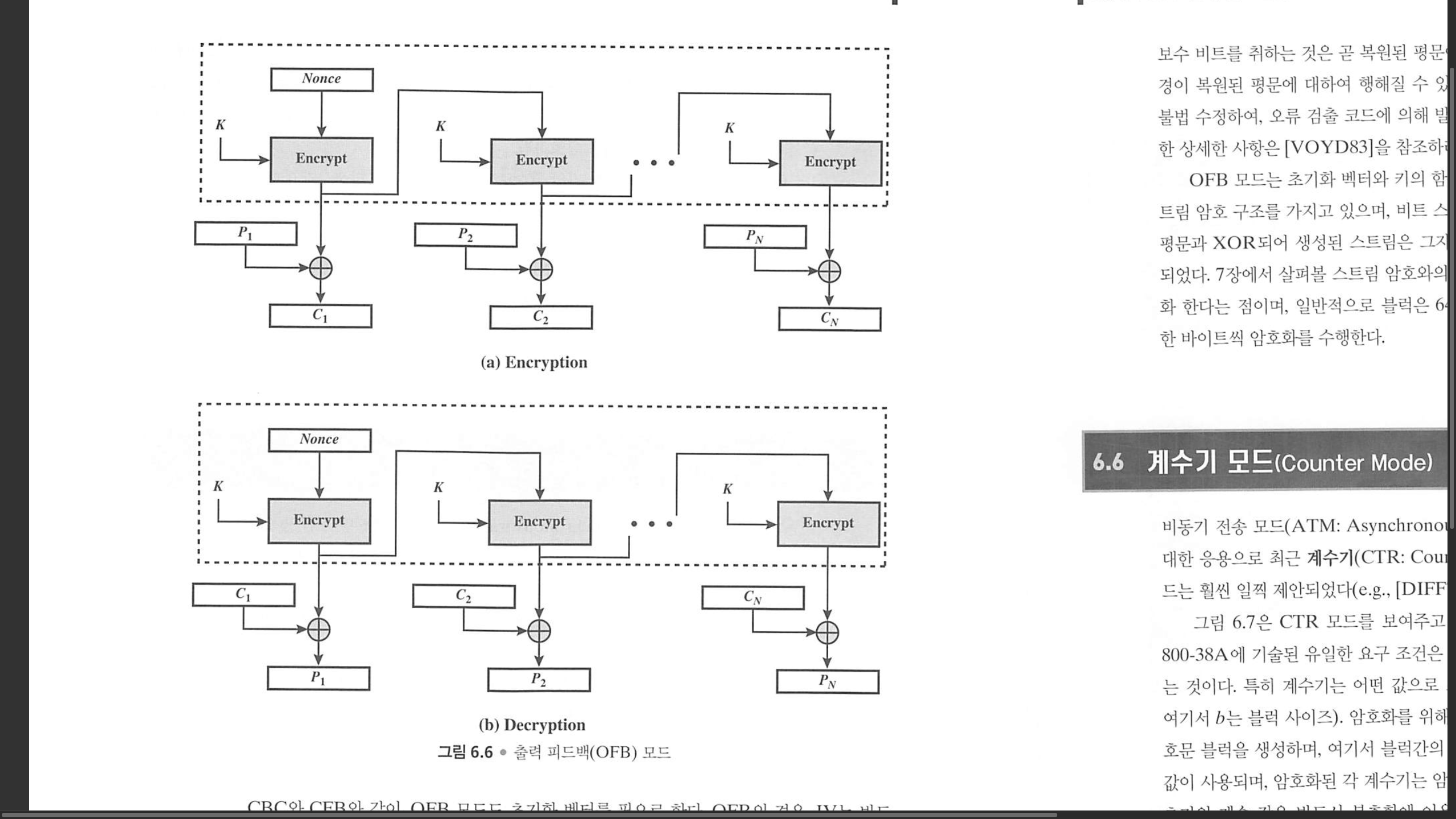
  • OFB 모드 (output feedback, 출력 피드백)
    블록 암호를 동기식 스트림 암호로 변환한다.
    XOR 명령의 대칭 때문에 암호화와 복호화 방식은 완전히 동일하다.

OFB

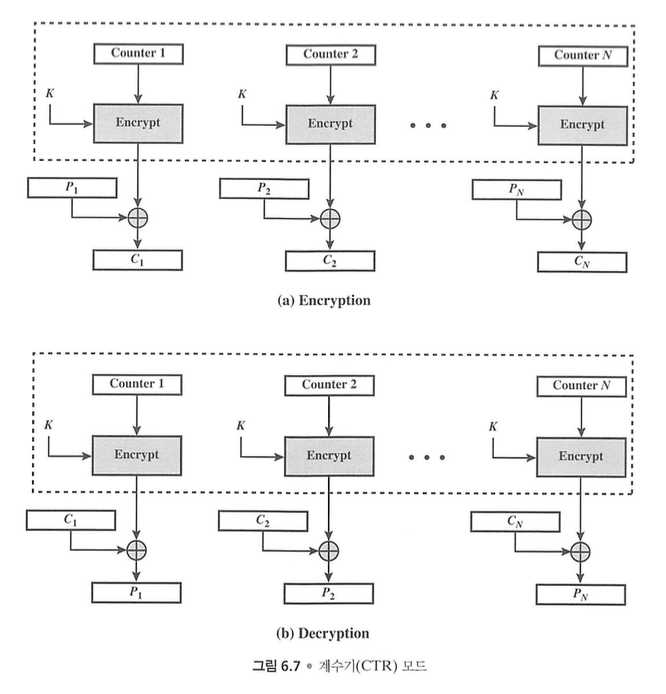
CTR 모드 (Counter, 카운터)
블럭 암호를 스트림 암호를 바꾸는 구조를 가진다.
카운터 방식에서는 각 블록마다 현재 블록이 몇 번째인지 값을 얻어, 그 숫자와 nonce 를 결합하여 블록 암호의 입력으로 사용한다.
그렇게 각 블록 암호에서 연속적인 난수를 얻은 다음 암호화하려는 문자열과 XOR 한다.
카운터 모드는 각 블록의 암호화 및 복호화가 이전 블록에 의존하지 않으며, 따라서 병렬적으로 동작하는 것이 가능하다.

CTR

블록암호와 운용방식(ECB, CBC, CTR)

블록암호 (block cipher) 란 기밀성 있는 정보를 고정된 크기의 블록단위로 구성하여 암호화 작업을 하는 대칭키 암호 시스템이다.
암호문은 평문의 반복되는 회전 함수로 생산되며 회전함수의 입력은 Key와 Output of Previous Round (전 번 회전 출력) 으로 구성된다.

이러한 블록 암호는 운용방식이 존재하는데 만약 암호화 하려 하는 데이터가 블록 길이보다 길 경우에는 특정한 운용방식이 사용되게 된다. Ex) ECB/CBC/CTR 등

  • 블록 암호 운용 방식

블록 암호 운용방식은 하나의 키 하에서 블록 암호를 반복적으로 안전하게 이용할 수 있도록 하는 절차를 이야기 합니다. 블록 암호는 특정한 길이의 블록 단위로 동작하기 때문에, 가변 길이 데이터를 암호화하기 위해서는 먼저 이들을 단위 block 들로 나누어야 하며, 그 블록들을 어떤 암호화 작업을 거칠지 정해야 한다. 이때 블록들의 암호화 방식을 운용 방식이라고 한다.

운용 방식은 주로 암호화와 인증을 목적으로 정의되어 있으며 운용 방식이 일반적으로 대칭형 암호화와 관련하는 것이 일반적이지만 RSA 와 같은 공개키 암호화 알고리즘에도 적용할 수 있다.

  • ECB (Electronic Codebook)
    운용 방식 중 가장 간단한 구조를 가지며, 암호화 작업을 하려는 메세지를 여러 블록으로 나누어 각각 암호화하는 방식이다.

전자 코드북은 모든 블록이 같은 암호화 키를 사용하기 때문에 보안에 취약하다. 만약 암호화 메세지를 여러 부분으로 나누었을 때 두블록이 같은 값을 가진다면, 암호화한 결과값도 같다.
이것은 공격자가 비슷한 메세지를 반복적으로 암호화하는 공격에도 취약하며 대표적으로 복사/붙여넣기 공격이 있다.

  • ECB 요약

  • 가장 단순한 모드로 블록단위로 순차적으로 암호화하는 구조
  • 한 개의 블록만 해독되면 나머지 블록도 해독이 되는 단점
  • 암호문이 블록의 배수가 되기 때문에 복호화 후 평문을 알기 위해서 Padding 이 필요

  • 각 블록이 독립적으로 동작하므로 한 블록에서 에러가 발생해도 다른 블록에 영향을 주지 않음. 해당 블록까지만 에러 전파

  • CBC (Cipher-block chaining)
    암호 블록 체인 방식은 1976년 IBM에 의해 개발되었으며 각 블록은 암호화 되기 전에 이전 블록의 암호화 결과와 XOR 연산을 수행하며, 첫 블록의 경우 IV(초기화 벡터)를 사용한다.
    초기화 벡터의 경우 출력 결과가 항상 동일하기 때문에, 매 암호화마다 다른 IV를 사용해야 한다.

CBC 방식은 현재 널리 사용되는 운용 방식이며 CBC는 암호화 입력값이 이전 결과에 의존하기 때문에 병렬화가 불가능하지만, 복호화의 경우 각 블록을 복호화 한 다음 이전 아호화 블록과 XOR 연산을 통해 복구할 수 있으므로 병렬화가 가능하다.

  • CBC 요약

  • 블록 암호화 운영 모드 중에서 보안성이 가장 높은 암호화 방법으로 널리 사용
  • 평문의 각 블록은 XOR 연산을 통해 이전 암호문과 연산되고 첫 번째 암호문에 대해서는 IV가 암호문 대신 사용되며, 이때 IV는 제 2의 키가 될 수 있음
  • 암호문이 블록의 배수가 되기 ㅐ문에 복호화 후 평문을 얻기 위해서 Padding 을 해야 함
  • 암호화가 병렬처리가 아닌 순차적으로 수행되어야 함

  • 깨진 암호문의 해당블록과 다음 블록의 평문까지 영향을 미치게 됨

  • CTR (Counter)
    카운터 방식은 블록 암호를 스트림 암호 (Stream Cipher)로 바꾸는 구조를 가진다. 카운터 방식에는 각 블록마다 현재 블록이 몇 번째인지 값을 얻어, 그 숫자와 nonce 를 결합하여 블록 암호의 입력으로 사용한다.
    그렇게 각 블록 암호에서 연속적인 난수를 얻은 후 암호화하려는 문자열과 XOR 연산을 한다. 카운터 모드는 각 블록의 암호화 및 복호화가 이전 블록에 의존하지 않으므로 병렬처리가 가능하며 암호화된 문자열에서 원하는 부분만 복호화도 가능하다.

  • CTR 요약

  • 블록을 암호화 작업을 거칠 때마다 1씩 증가하는 카운터를 암호화해서 Key Stream 을 생성, 즉 카운터를 암호화한 비트열과 평문블록과의 XOR 연산을 취한 결과가 암호문 블록이 된다.
  • CTR 모드는 스트림 암호의 일종
  • CTR 모드의 암/복호화는 완전히 같은 구조가 되므로 구현이 간단하다.
  • CTR 모드에서는 블록의 순서를 임의로 암/복호화 할 수 있다.
  • 블록을 임의의 순서로 처리할 수 있다는 것은 병렬처리가 가능하다는 의미
  • 각 블록이 병렬처리 되므로 같은 블록 내에서만 이루어진다.

7장. 의사 난수 생성과 스트림 암호

제 13장 난수 - 박종혁 교수

난수의 용도

  1. 키 생성 - 대칭 암호나 메세지 인증 코드
  2. 키 쌍 생성 - 공개 키 암호나 디지털 서명
  3. 초기화 벡터(IV) 생성 - 블록 암호 모드인 CBC, CFB, OFB
  4. 비표(nonce) 생성 - 재전송 공격 방지나 블록 암호의 CTR 모드
  5. 솔트 생성 - 패스워드를 기초로 한 암호화 (PBE)
  6. 일회용 패드 - 패딩에 사용되는 열을 생성
  • 아무리 강한 암호 알고리즘이라도 키가 공격자에게 알려져 버리면 아무 의미가 없다
  • 난수를 사용해서 키를 만들어, 공격자에게 키를 간파당하지 않도록 하는 것
  • 난수를 사용하는 목적은 간파 당하지 않도록 하기 위한 것

2.1 난수의 성질 분류

  • 무작위성

  • randomness

  • 통계적인 편중이 없이 수열이 무작위로 되어 있는 성질

  • 예측 불가능성

  • unpredictability

  • 과거의 수열로부터 다음 수를 예측할 수 없다는 성질

  • 재현 불가능성

  • reconstruction is impossible
  • 같은 수열을 재현할 수 없다는 성질
  • 재현하기 위해서는 수열 그 자체를 보존해야만 하는 성질
  무작위성 예측 불가능성 재현 불가능성 비고 암호 기술 적용 가능 여부 :
약한 의사난수 O X X 무작위성만 갖는다 암호 기술에 사용할 수 없다
강한 의사난수 O O X 예측 불가능성도 갖는다 암호 기술에 사용할 수 있다
진정한 난수 O O O 재현 불가능성도 갖는다 암호 기술에 사용할 수 있다

2.2 무작위성 (Randomness)

  • <아무렇게> 보이는 성질

  • 의사난수열의 통계적인 성질을 조사해서 치우침이 없도록 하는 성질

  • 난수 검정
    .의사난수열의 무작위성을 조사하는 것

  • 암호 기술에 사용하는 난수는 무작위성을 가지고 있는 것만으로는 불충분

  • 약한 의사난수
    .무작위성만을 갖는 의사난수

2.3 예측 불가능성 (Unprecictability)

  • 공격자에게 간파 당하지 않는다는 예측 불가능성이 필요
  • 과거에 출력한 의사난수열이 공격자에게 알려져도 다음에 출력하는 의사난수를 공격자는 알아맞힐 수 없다는 성질

  • 알고리즘은 공격자에게 알려져 있다고 가정하고 Seed를 사용

  • 시드 (Seed): 공격자에게 비밀

  • 약한 의사난수

  • 무작위성만을 갖는 의사난수

  • 강한 의사난수

  • 예측 불가능성을 갖는 의사난수
  • 예측 불가능성을 가지면 당연히 무작위성을 가짐

2.4 재현 불가능성

  • 한 난수열이 주어졌을 때 동일한 수열을 재현할 수 없는 성질
  • 재현하기 위해서는 그 난수열 자체를 보존해두는 것 이외에 방법이 없는 성질
  • 소프트웨어만으로는 재현 불가능성을 갖는 난수열 생성 불가

  • 소프트웨어는 의사난수열만 생성가능

  • 소프트웨어가 돌아가는 컴퓨터가 유한의 내부 상태밖에 없기 때문

주기

  • 소프트웨어가 생성하는 수열은 언젠가는 반복
  • 주기 (period): 반복이 다시 시작할 때까지의 수열의 길이
  • 주기를 갖는 수열은 재현 불가능하지 않음

재현 불가능한 난수 생성

  • 재현 불가능한 물리 현상으로부터 정보를 취득

  • 주위의 온도나 소리의 변화
  • 사용자의 마우스 위치 정보
  • 키스트록 입력 시간 간격
  • 방사선 관측기의 출력

  • 다양한 하드웨어로부터 얻어진 정보

  • 진성난수 (Real Random Number):

  • 재현 불가능한 난수
  • 위의 3 가지 성질을 모두 가진다
    .무작위성
    .예측 불가능성
    .재현 불가능성
    ex) 동전 던지기 결과로 얻어지는 비트, 앞-0 뒤-1

3.1 의사난수 생성기의 구조

  • 난수 생성기 (random number generator; RNG)

  • 하드웨어로 생성

  • 의사난수 생성기 (pseudo random number generator; PRNG)

  • 소프트웨어로 생성
  • 주기성을 가짐

Blum Blum Shub 생서기

Blum Blum Shub 생성기

  • 개발자들의 이름에서 유래 [BLUM86]
  • 어떠한 특정 목적의 알고리즘에서도 암호학적 강도를 증명하는 가장 강력하게 통용되는 수단
  • 암호학적으로 안전한 의사난수 비트 생성기로 불림
    • CSPRBG: Cryptographically Secure Pseudo Random Bit Generator
  • Iterative equation 에서 least significant bit 사용
  • Is unpredictable given any run of bits
  • Slow, since very large numbers must be used
  • Two slow for cipher use, good for key generation
  • n의 소인수 분해 문제에 대한 어려움에 기반 - n이 주어졌을 때, n의 두 소수 인수 p와 q를 알아야 함

의사 난수 생성의 원리

  • TRNG(True Random Number Generator: 진 난수 생성기)

  • 실제적으로 랜덤한 소스를 입력으로 사용
    .키보드 입력 타이밍 패턴 및 마우스 움직임
    .디스크의 전기적 활동, 시스템 클럭의 순간 값

  • PRNG(Pseudo Random Number Generator: 의사난수발생기)

  • 고정값 seed를 입력받아 결정적 알고리즘을 사용하여 출력 비트열 생성

  • 제한이 없는 비트열 생성하는 데 사용
    .알고리즘과 시드를 알고 있는 공격자는 비트열 재생성 가능

  • PRF(Pseudo Random Function: 의사난수 함수)

  • 고정된 길이의 의사 난수 비트열을 생산하는 데 사용

PRNG 요구 사항

  • Seed 를 알지 못하는 공격자가 의사 난수열을 결정할 수가 없어야 함

  • 임의성 (Randomness)

  • 생성된 비트 스트림이 결정적일 지라도 랜덤하게 보여야 함
  • 균일성 (난수 또는 의사 난수 비트열의 생성에 있어서 0과 1은 거의 동일하게 존재)
  • 확장성 (비트열이 랜덤하면 무작위로 추출된 어떤 비트열도 랜덤해야 함)
  • 일관성 (생성기의 동작은 초기값 전반에 대해 일관되어야 함)
  • 비예측성 (Unpredictability)
    수열의 잇따른 다음 수의 순서에 대해 예측이 불가능해야 함
    전 방향 비예측성 - 이전 비트들에 대한 정보가 있다고 하더라도 다음 출력 비트는 예측할 수 없어야 함
    후 방향 비예측성 - 생성된 어떠한 값의 정보를 통해서도 seed를 결정할 수 없어야 함
  • 시드 요구사항 (Seed Requirements)
    Seed 는 예측 불가능해야 함
    Seed 는 난수 또는 의사난수이어야 함
    TRNG 에 의해 seed 생성 - SP800-90 에서 권고 (NIST)

3.1 의사난수 생성기의 구조

  • 내부 상태
  • 시드 (Seed)
    seed
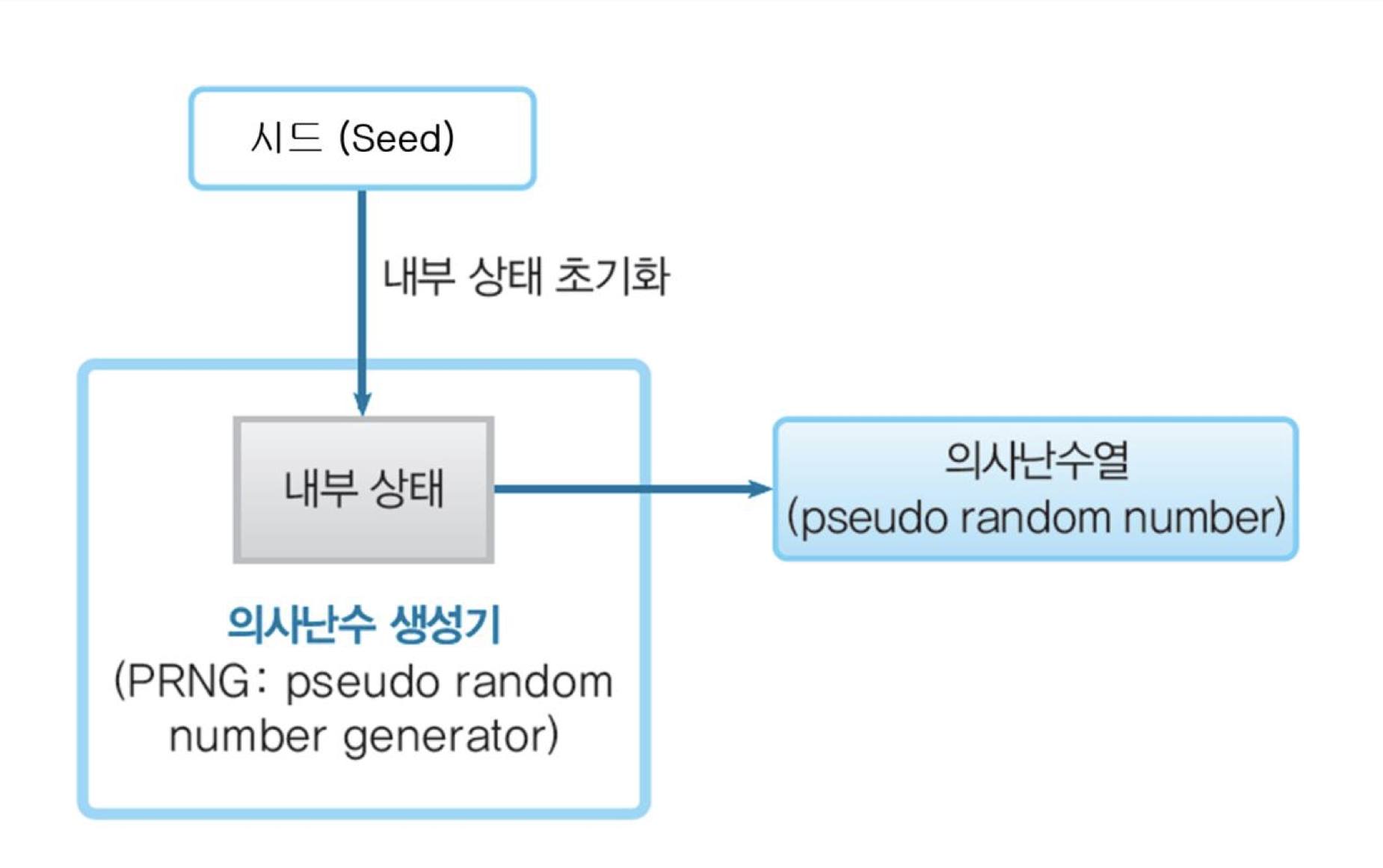
  • 의사난수 생성기가 관리하고 있는 메모리 값
  • 의사난수 생성기는 메모리의 값(내부 상태)을 기초로 해서 계산을 수행
  • 그 계산 결과를 의사난수로서 출력
  • 다음 의사난수의 요구에 대비해서 자신의 내부 상태를 변화

의사 난수 생성 알고리즘

  • 의사난수 생성 알고리즘의 2가지 기능

  • 의사난수를 계산하는 방법
  • 내부 상태를 변화시키는 방법

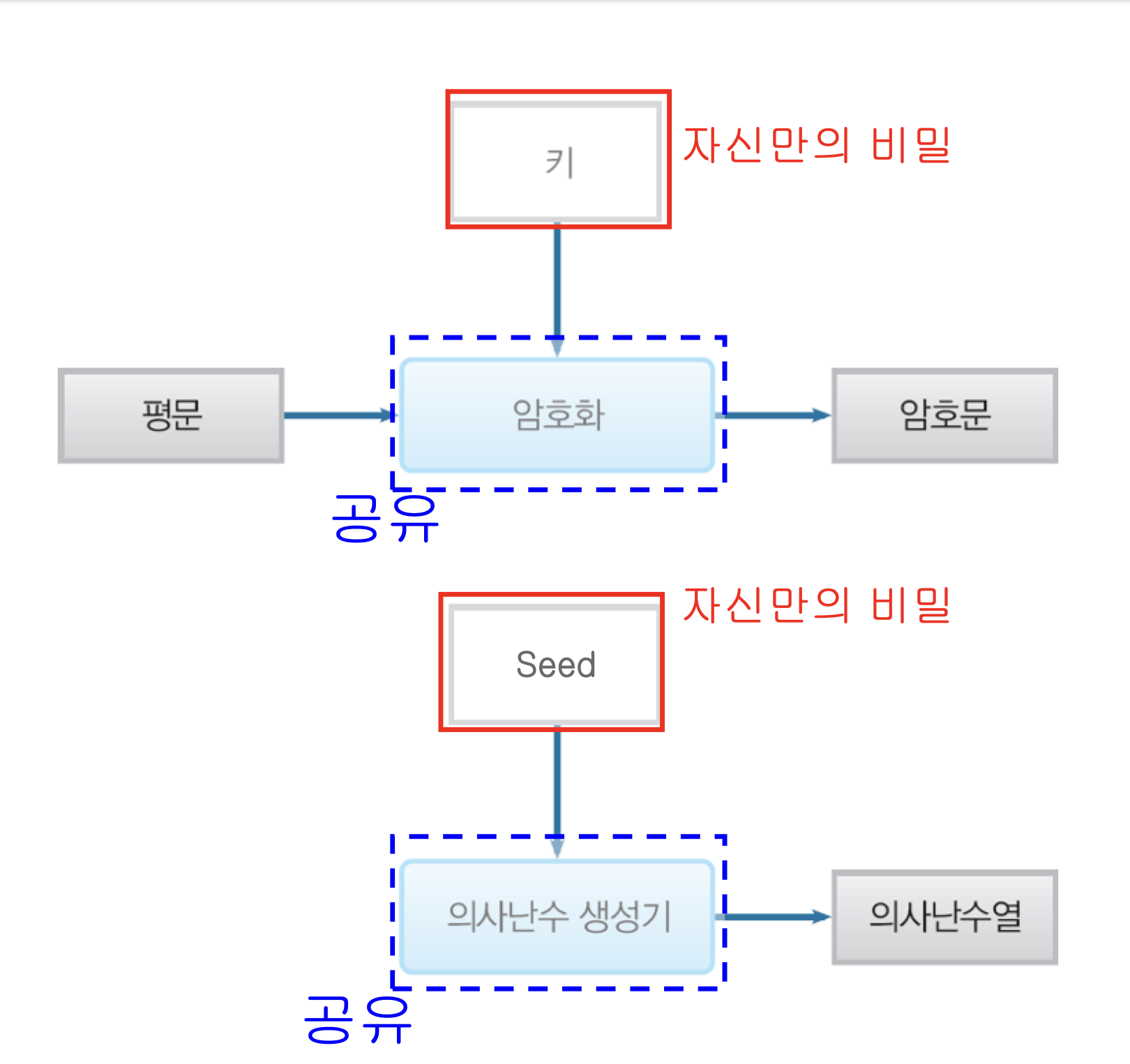
의사난수 생성기의

  • 의사난수 생성기의 내부 상태 초기화에 필요
  • 랜덤한 비트 열
  • Seed는 자신만의 비밀로 유지
    seed2

4.1 무작위 방법

  • 긴 주기:

  • 암호 기술에서 사용하는 난수는 예측 불가능성을 가져야 하므로 주기가 짧아서는 안됨

  • 복잡한 알고리즘 보다는 명확한 알고리즘
    -프로그래머가 자세한 내용을 이해할 수 없는 알고리즘으로 생성한 난수는 예측 불가능성을 갖는지 어떤지 평가를 할 수 없음

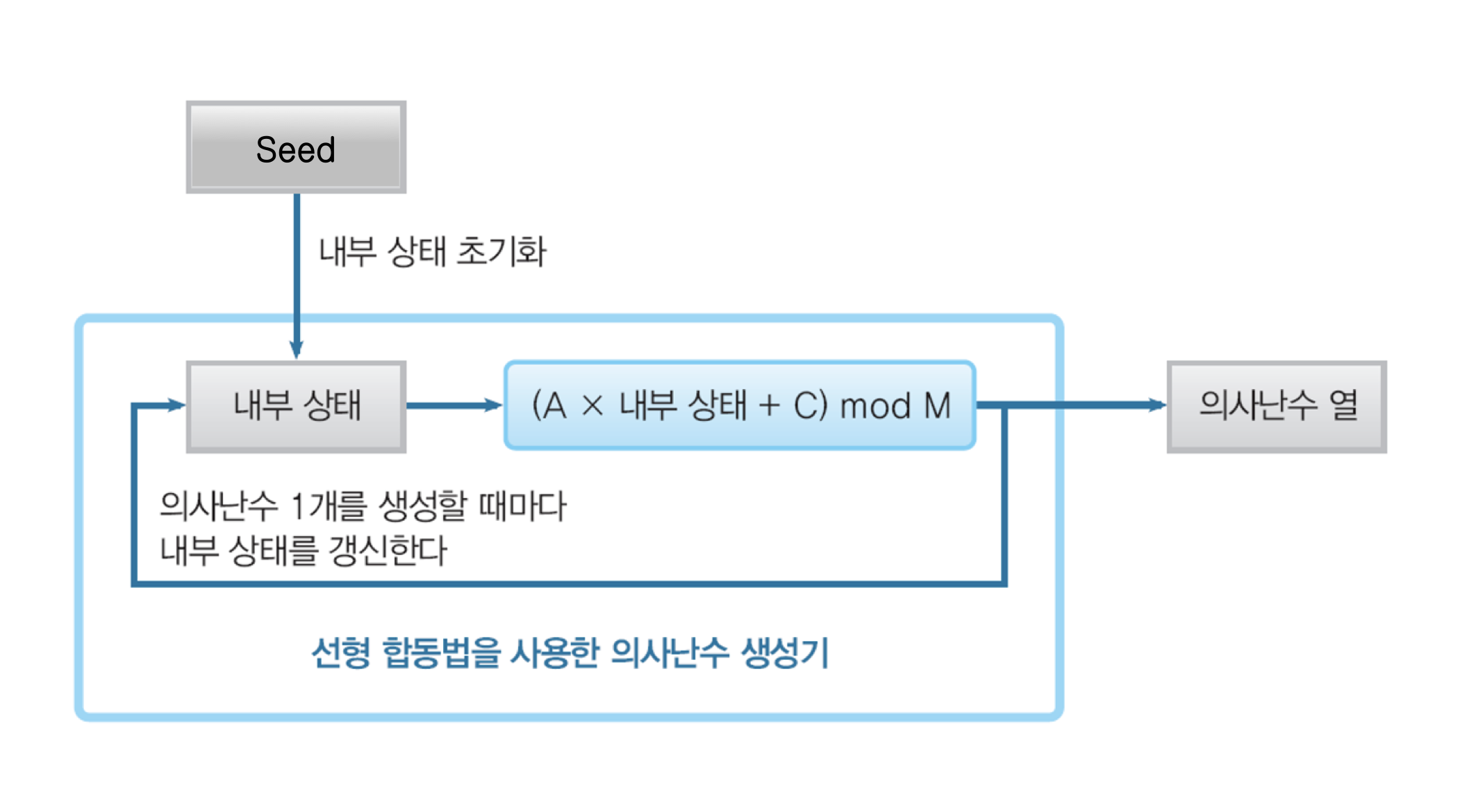
4.2 선형 합동법

  • 선형 합동법 (linear congruentialmethod)

  • 일반적으로 가장 많이 사용되는 의사난수 생성기
  • 암호 기술에 사용하면 안됨 (“예측 불가능성”이 없음)
  • 현재 의사난수의 값을 A배하고 C를 더한 다음, M으로 나눈 나머지를 다음 의사난수로 선택

선형 합동법 계산 방법

  • R(0) 생성:

  • 최초 의사난수 R0 = (A x Seed + C) mod M

  • A,C,M은 정수이고, A와 C는 M보다도 작은 수

  • R(1) 생성:

  • R1 = (A x R0 + C) mod M

  • R(n+1) 생성:

  • R(n+1) = (A x Rn + C) mod M
  • n = 2, 3, …

seed3

선형 합동법 예

 A = 3
 C = 0
 M = 7

 R0 = (A x Seed + C) mod M
    = (3 x 6 + 0) mod 7
    = 18 mod 7
    = 4

 R1 = (A x R0 + C) mod M
    = (3 x 4 + 0) mod 7
    = 12 mod 7
    = 5

 R2 = (A x R1 + C) mod M
    = (3 x 5 + 0) mod 7
    = 15 mod 7
    = 1

 R3 = (A x R2 + C) mod M
    = (3 x 1 + 0) mod 7
    = 3 mod 7
    = 3
  • 반복해서 4, 5, 1, 3, 2, 6, 4, 5, 1, 3, 2, 6, … 생성
  • 이 경우 4, 5, 1, 3, 2, 6 이라는 6개 숫자의 반복이 되므로 주기는 6
  • 의사난수의 값은 M으로 나눈 나머지이므로, 반드시 0부터 M-1 의 범위
  • A와 C와 M의 값에 따라 다른 주기를 가짐

  • 예) A = 6, C = 0, M = 7, Seed = 6 인 경우

  • 의사난수열은 1, 6, 1, 6, 1, 6, …

  • 주기는 2

  • A값 변화에 따른 의사난수열
  • A = 0 인 경우: 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … (주기는 1)
  • A = 1 인 경우: 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, … (주기는 1)
  • A = 2 인 경우: 5, 3, 6, 5, 3, 6, 5, 3, 6, 5, , … (주기는 3)
  • A = 3 인 경우: 4, 5, 1, 3, 2, 6, 4, 5, 1, 3, … (주기는 6)
  • A = 4 인 경우: 3, 5, 6, 3, 5, 6, 3, 5, 6, … (주기는 3)
  • A = 5 인 경우: 2, 3, 1, 5, 4, 6, 2, 3, 1, 5, … (주기는 6)
  • A = 6 인 경우: 1, 6, 1, 6, 1, 6, 1, 6, 1, 6, … (주기는 2)

선형합동법의 단점

  • 선형 합동법은 예측 불가능성이 없다

  • 선형 합동법을 암호 기술에 사용해서는 절대로 안됨

  • 예: 선형 합동법을 사용하는 함수 (C 라이브러리 함수 rand, Java 의 java.util.Random 클래스)
  • 이들을 암호 기술에서 사용해서는 안됨

선형 합동법의 예측불가능성 테스트 (공격)

  • 공격자가 A = 3, C = 0, M = 7 이라는 값을 알고 있다고 가정
  • 공격자가 생성된 의사난수를 1개라도 손에 넣는다면 그 다음에 생성되는 의사난수를 예측하는 것이 가능
  • 입수한 의사난수 R을 이용, 다음을 계산 (A x R + C) mod M = (3 x R + 0) mod 7
  • 공격자는 의사난수의 Seed: 6을 알 필요가 없다
  • 위에서 수행한 계산이 반복으로 이후 생성되는 의사난수열을 모두 예측 가능

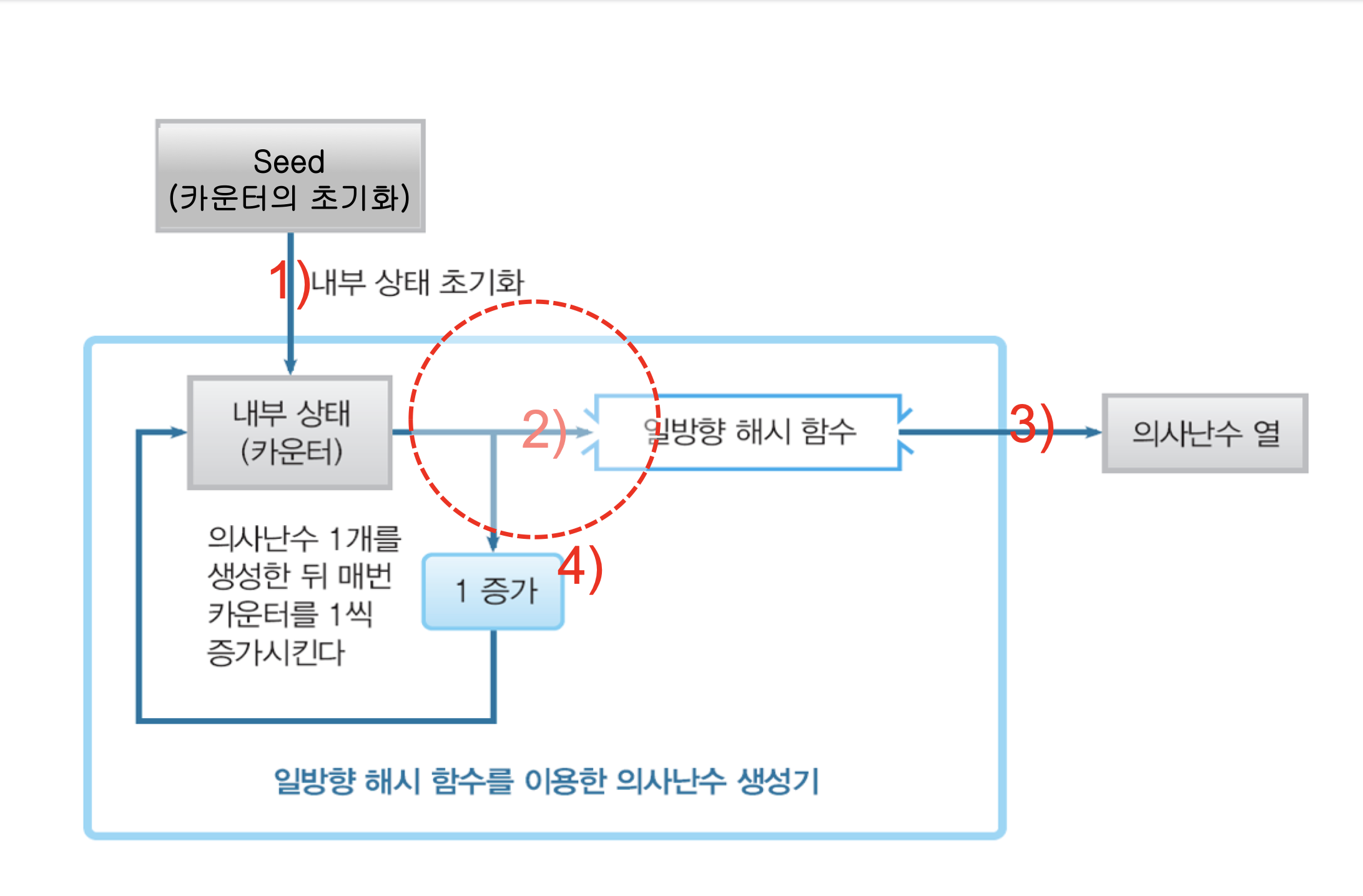
4.3 일방향 해시 함수를 사용하는 방법

  • 일방향 해시 함수 (예, SHA-1)를 사용해서 예측 불가능성을 갖는 의사난수 열 (강한 의사난수)을 생성하는 의사난수 생성기를 만들 수 있다
  • 일방향 해시 함수의 일방향성이 의사난수 생성기의 예측 불가능성을 보장

절차

  1. 의사난수의 Seed를 사용해서 내부 상태(카운터)를 초기화
  2. 일방향 해시 함수를 사용해서 카운터의 해시 값 생성
  3. 그 해시 값을 의사난수로서 출력
  4. 카운터를 1 증가
  5. 필요한 만큼의 의사난수가 얻어질 때까지 (2) ~ (4) 를 반복

seed4

4.4 잘못 만들어진 의사난수 생성기

  • 다음과 같이 생성했다고 해보자
  1. 의사난수의 Seed를 사용해서 내부 상태를 초기화한다.
  2. 일방향 해시 함수를 사용해서 내부 상태의 해시 값을 얻는다.
  3. 해시 값을 의사난수로서 출력한다.
  4. 그 해시 값을 새로운 내부 상태로 한다.
  5. 필요한 만큼의 의사난수가 얻어질 때까지 (2) ~ (4) 를 반복한다.

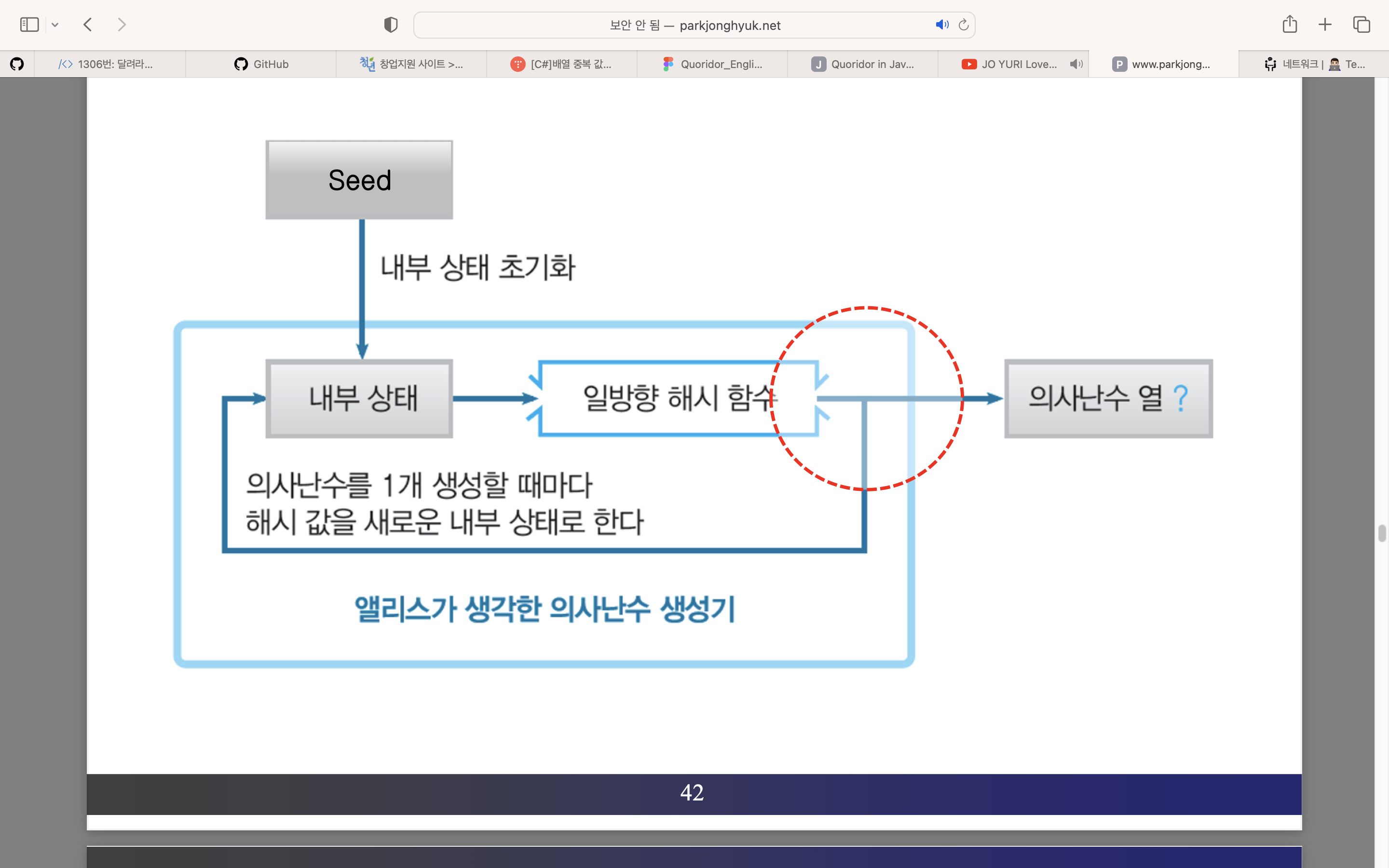
seed5

왜 예측 불가능성이 없나?

  • 마지막에 출력한 의사난수의 해시 값을 취해서 다음 의사난수를 생성하므로 예측 불가능성을 갖지 않는다.
  • Why? - 예측 불가능성을 갖기 위해서는 일방향 해시 함수의 일방향성을 사용하는 것이 포인트

4.5 암호를 사용하는 방법

  • 암호를 사용해서 <강한 의사난수="">를 생성하는 의사난수 생성기를 만들 수 있다
  • AES 와 같은 대칭 암호나 RSA 와 같은 공개 키 암호 중 어느 것을 사용해도 무방
  • 암호의 기밀성이 의사난수 생성기의 예측 불가능성을 보장
  • 블록 암호 운용 모드를 이용한 PRNG
    • CTR 모드: SP800-90, ANSI 표준 X9.82(난수 생성), RFC4086
    • OFB 모드: X9.82, RFC4086

암호를 사용한 의사난수생성 절차

  1. 내부 상태(카운터)를 초기화
  2. 키를 사용해서 카운터를 암호화
  3. 그 암호문을 의사난수로서 출력
  4. 카운터를 1 증가
  5. 필요한 만큼의 의사난수가 얻어질 때까지 (2) ~ (4)

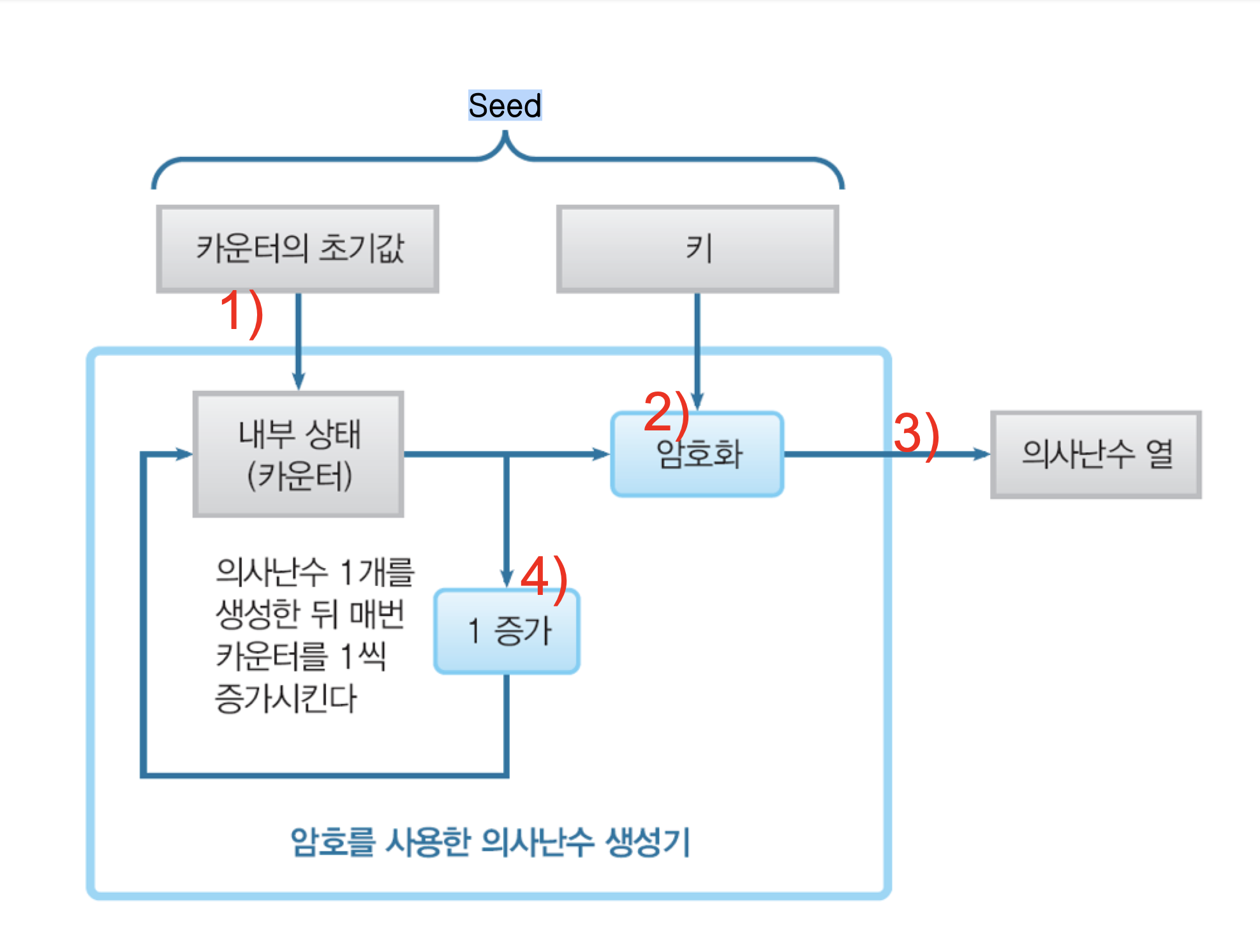
seed6

4.5 ANSI X9.17

  • 암호 소프트웨어 PGP 에서 사용하는 의사난수 생성기

  • ANSI X9.17

  • ANSI X9.31

  • ANSI X9.17 의사 난수 생성기

  • 입력: 현재의 날짜와 시간 (64비트), seed 값
  • 키: 3개의 3-DES 모듈 사용, 동일한 56 비트 키 쌍 사용
  • 출력: 64비트 의사난수와 64비트 seed 값으로 구성

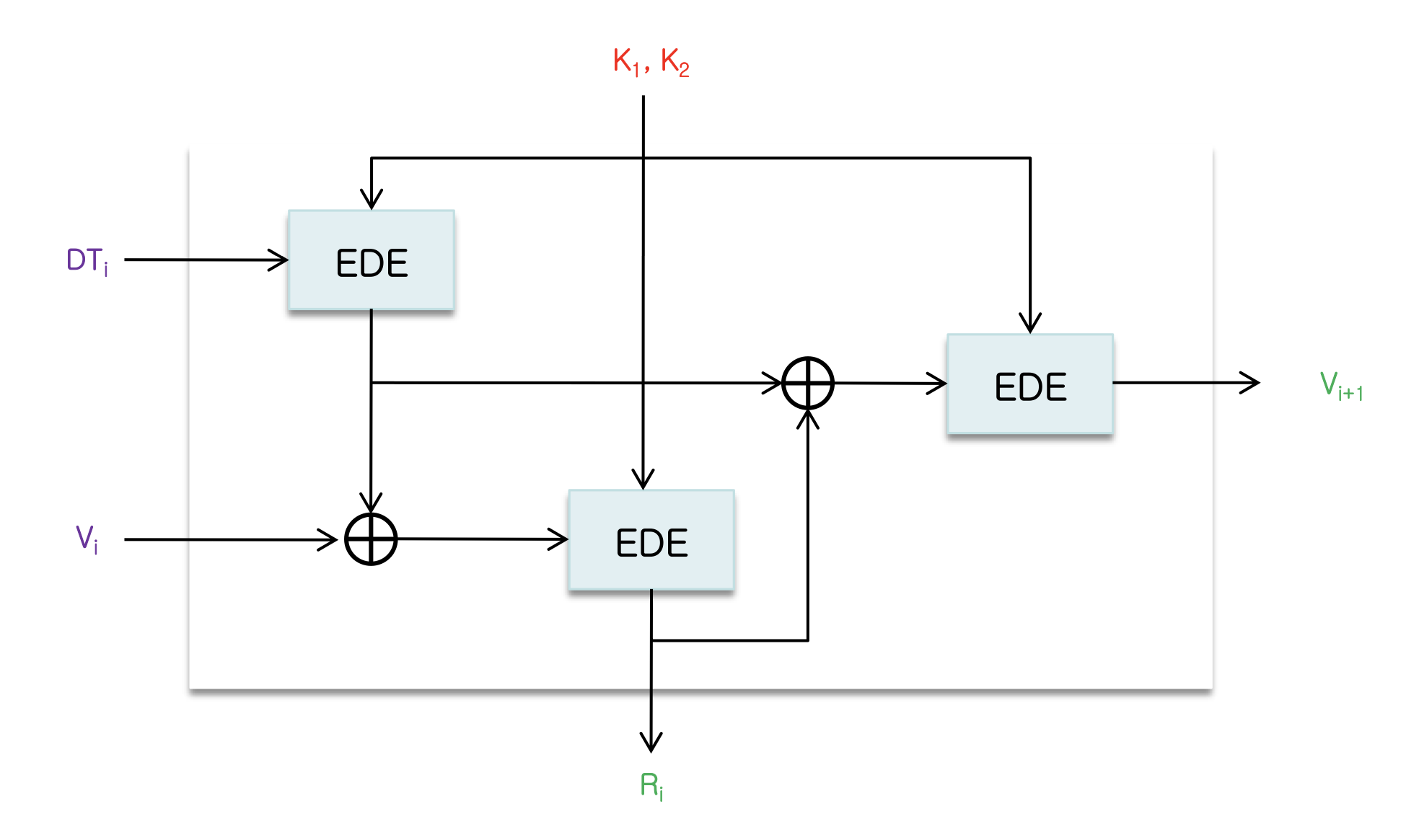
seed7

ANSI X9.17 의사난수 생성 절차

  1. 내부 상태를 초기화
  2. 현재 시각을 암호화
  3. 내부 상태와 암호화된 현재 시각을 XOR
  4. 절차(3)의 결과를 암호화
  5. 절차(4)의 결과를 의사난수로서 출력
  6. 절차(4)의 출력과 암호화된 현재시각을 XOR
  7. 절차(6)의 결과를 암호화
  8. 절차(7)의 결과를 새로운 내부 상태로 설정
  9. 절차(2)~(8) 을 필요한 만큼의 의사난수가 얻어질 때까지 반복

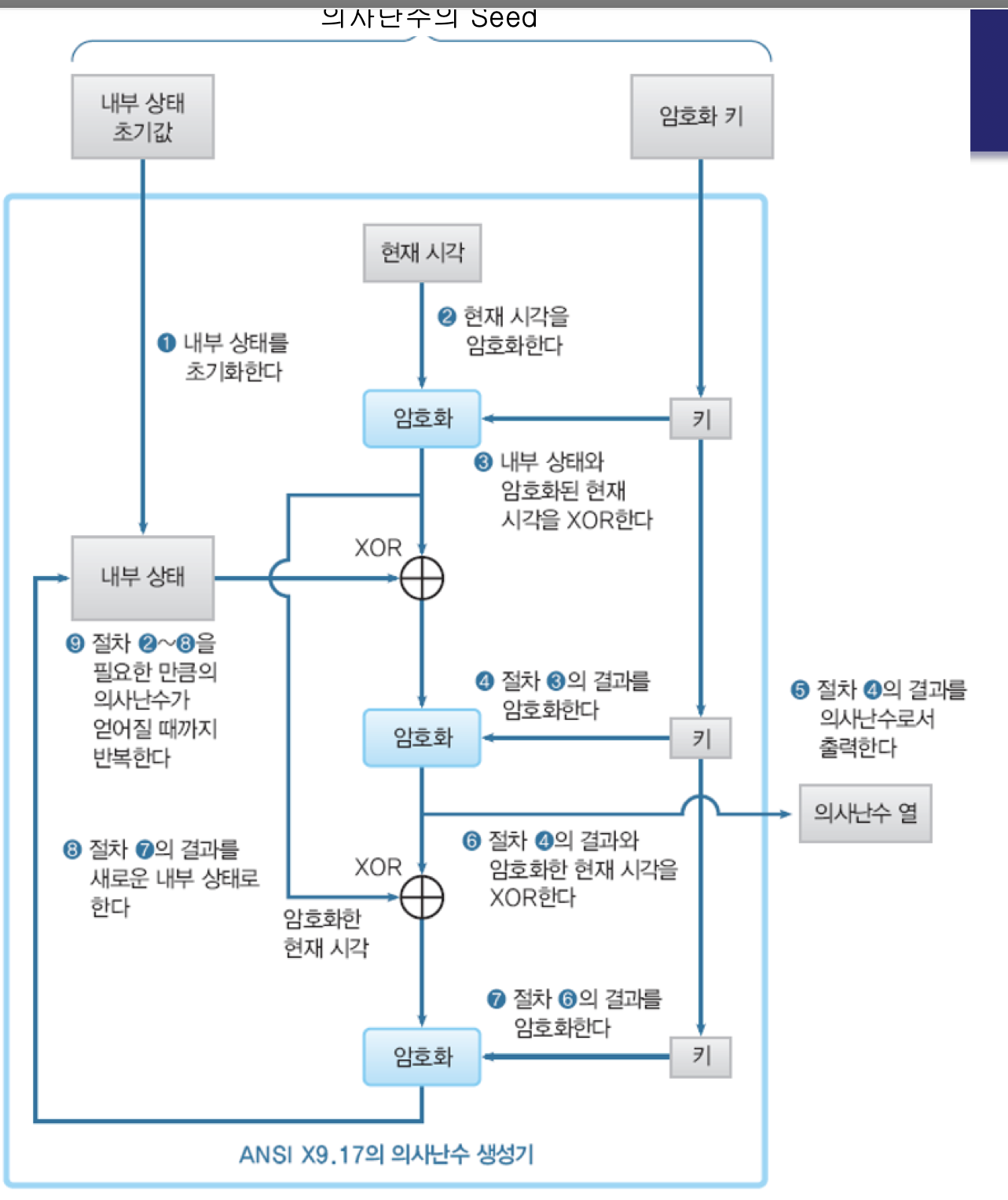
seed8

왜 내부 상태 추측을 못하나?

  • 공격자는 의사난수로부터 역산해서 [내부 상태와 암호화된 현재 시각의 XOR]을 간파할 수 없다

  • 이유: 간파하기 위해서는 암호를 해독해야만 한다

  • 공격자는 지금까지 출력된 의사난수열로부터 의사난수 생성기의 내부 상태를 추측 못한다

4.6 기타 알고리즘

  • 알고리즘을 선택할 때 주의 점

  • 반드시 [이 난수 알고리즘은 암호나 보안 용도로 사용할 수 있는가]를 확인
  • 난수로 뛰어난 알고리즘이라 하더라도 예측불가능성을 갖추지 못한 것은 암호나 보안 용도로는 사용하면 안됨
  • 선형합동법은 충분한 길이의 난수열을 관찰하면 앞으로 생성될 난수열이 예측가능하므로 사용하면 안됨

RC4 암호 알고리즘

RC4 암호 알고리즘

대칭 키 암호에는 블록 암호와 스트림 암호가 있는데, 앞서 살펴본 AES와 DES는 대표적인 블록암호이다.
이번에는 스트림 암호에 대하여 알아보자.

  1. 스트림 암호 (Stream Cipher)
    연속적인 비트/바이트/단어들을 순차적으로 암호화하는 방식
    블록 암호는 일정한 크기의 데이터를 하나의 블록으로 묶어서 암호화했다면, 스트림암호는 묶지 않고, 별개의 데이터들에 순차적으로 암호화를 적용해주는 방식이다.

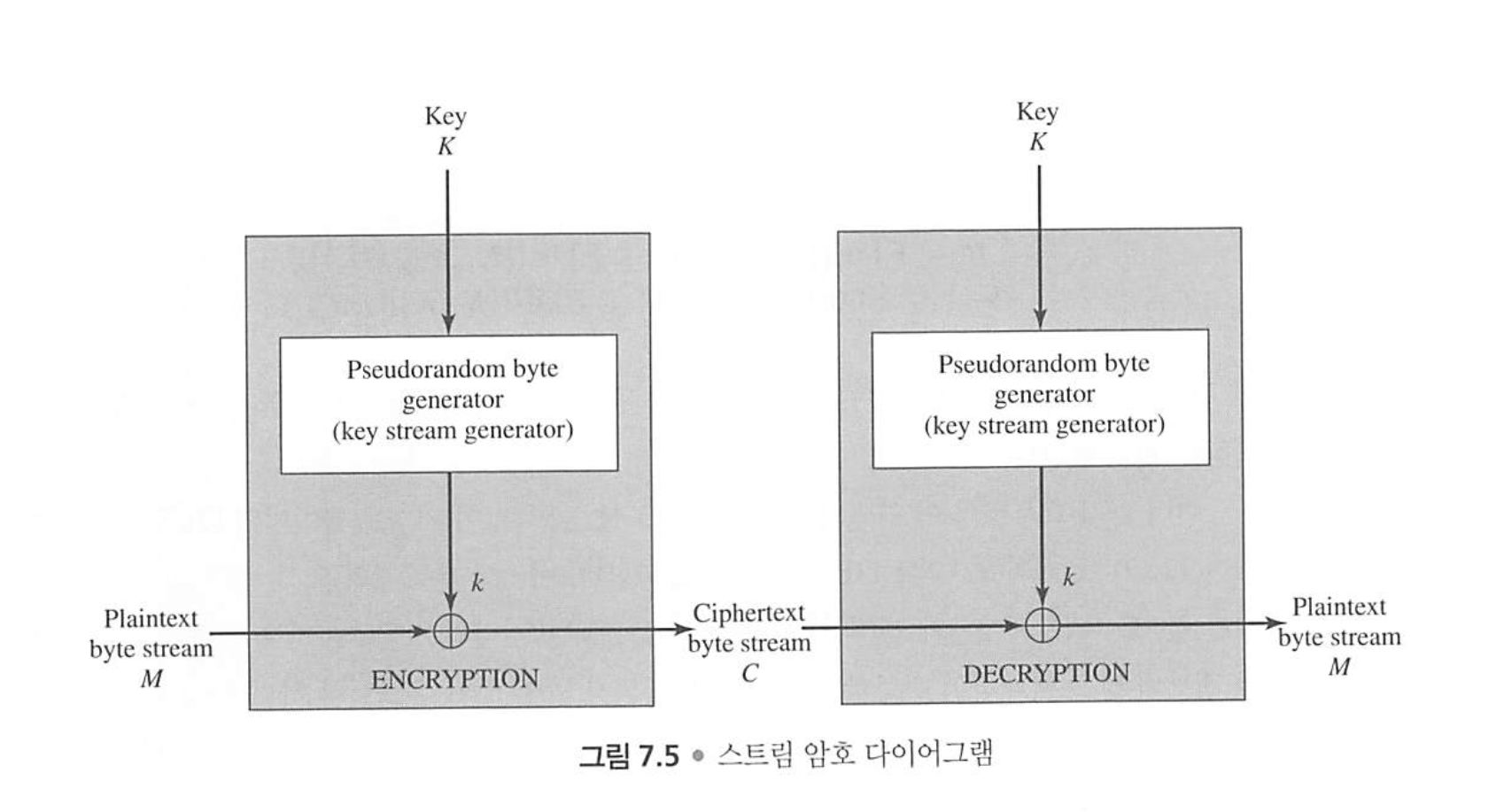StreamCiphers 주로 위의 그림과 같이 유사난수를 1비트 단위로 생성하고, 암호화하려는 데이터와 XOR하여 1비트의 암호문을 얻는 식으로 많이 사용된다.
스트림 암호는 블록 암호만큼 안전하며, 더 빠르고 간단하다는 특징이 있다.

RC4 는 SSL/TLS 나 네트워킹 프로토콜에서 자주 사용되는 스트림 암호기법으로, 굉장히 빠르다는 장점이 있다.
RC4 는 평문과 XOR 연산할 pseudorandom stream 을 만들어낸다. (Key stream) 그래서 RC4 자체를 난수 생성기로 사용할 수도 있다.

RC4는 상태(state) 개념을 사용한다.
S[0] S[1] S[2] S[3] ... S[255] 256 바이트로 구성된 상태(state)의 한 바이트는 암호화 키로서 사용되기 위해 랜덤하게 선택된다.

  • 초기화 단계 (The Key-scheduling Algorithm; KSA)

초기화는 우선, 256 바이트의 state vector 를 0, 1, 2, …, 255 로 초기화시킨다.
또한 키배열(K[0] K[1] K[2] … K[255]) 도 생성되는데, 이곳에는 키가 복사된다.
만약, 키의 길이가 256 바이트라면 그대로 복사시키고, 256 바이트보다 짧다면, 키배열이 꽉 찰 때까지 반복적으로 복사한다.
이제, 상태 배열과 키배열 256 바이트가 준비되어 있을 것이다. 이제, 키배열을 이용하여 상태배열을 swap 해준다..

  • The pseudo-random generation algorithm (PRGA)

이제 완벽히 뒤섞여진 상태배열 (S[0] S[1] S[2] … S[255]) 이 준비되어있을 것이다.

  1. 상태 배열은 두 개의 독립변수 i, j를 기반으로 swap될 것이다.
  2. i 번째와 j 번째의 두 상태 원소의 값은 키를 생성하기 위한 상태 배열의 인덱스를 정하기 위해 사용된다.

RC4

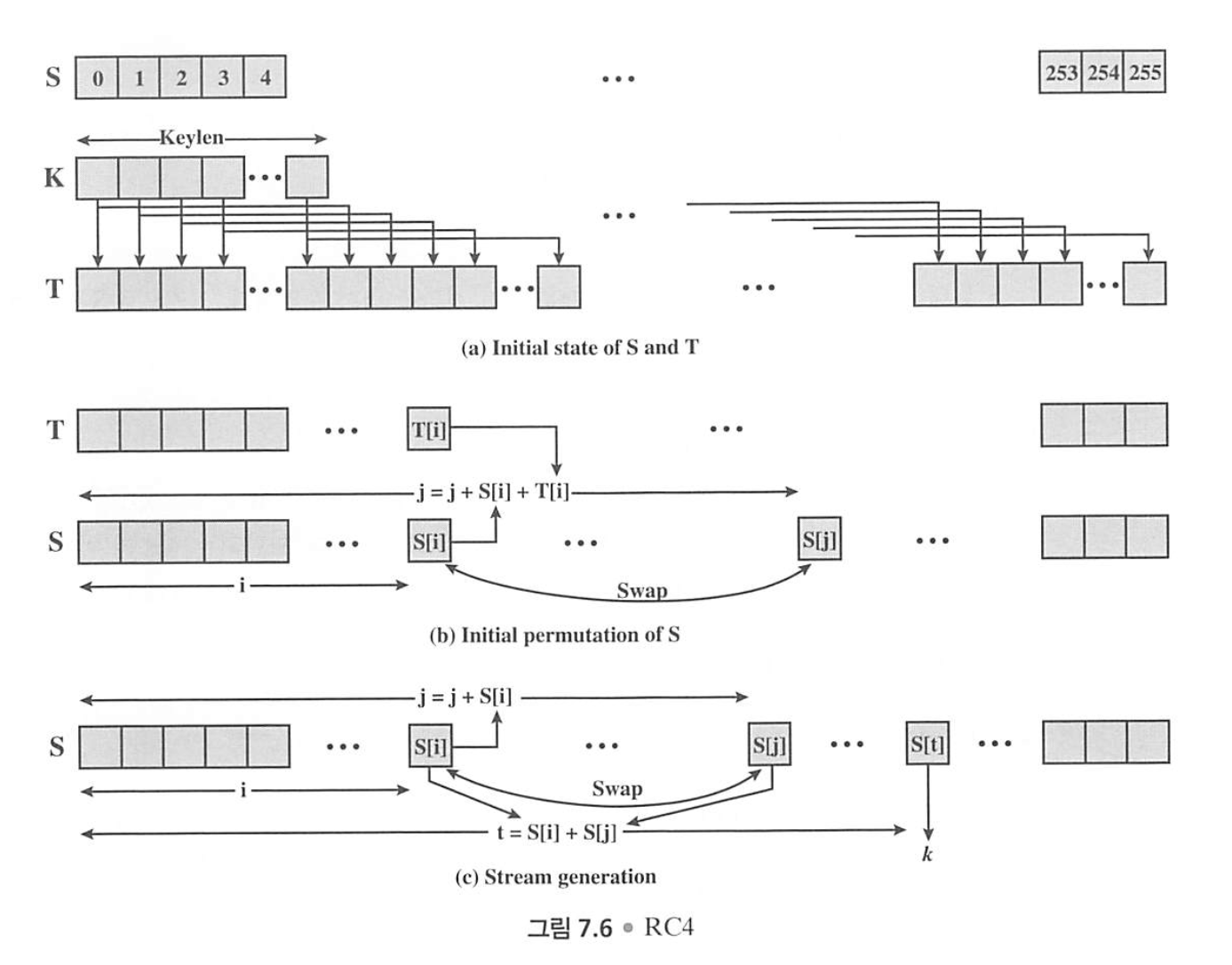
S[i] + S[j] 의 값에 해당하는 상태배열의 인덱스의 원소가 키다.
아무튼 상태배열의 원소는 1 바이트이므로 생성된 키도 1 바이트다. 이렇게 생성된 1 바이트 키를 가지고 1 바이트 평문을 암호화 시킨다.
평문이 끝날 때까지, 이 키 PRGA는 계속된다.(KSA는 처음 한 번만 시행한다)

  • RC4 의 안정성
    과거에는 정말 많은 분야에서 쓰였던 RC4 가 여러 가지 안정성 문제로 요즘에는 사용이 권장되지 않고 있다.
  1. RC4 로 생성된 키스트림의 일부값이 편향되게 나온다.
  2. 의사난수가 완벽한 난수가 아니므로 안정성 문제가 있다.

정리

  1. RC4는 대표적인 스트림 암호이다.
  2. RC4는 초기화 과정인 KSA, 1 바이트 키를 생성해내는 PRGA 과정으로 구성되어 있다.
  3. KSA는 한 번, PRGA 는 평문이 끝날 때까지 반복된다.
  4. RC4는 안전하지 않다.

4.7 진 난수 생성기

  • 엔트로피 소스 (Entropy Sources)

  • 진 난수 생성기는 임의성을 만들기 위해 비 결정적 소스 사용
    예측 불가능한 자연계의 처리 과정들을 측정하는 방법 사용 - 전리 방사선의 펄스 탐지기, 가스 방전광, 누전 축전기
    인텔 [JUN99] - 사용되지 않는 저항기들 사이에서 측정된 전압을 증폭시켜 열잡음을 샘플링하는 상업화된 칩 개발
  • 임의성의 소스 후보 [RFC 4086]
    음향/영상입력 - 실세계의 아날로그 소스를 디지털화하는 입력들을 가지고 작동
    디스크 드라이브 - 환경에 따라 회전 속도가 랜덤하게 변동되는 것을 측정
  • 편향 (skew)
    Deskewing 알고리즘 (편향 보정기법) - HW 장치에서 발생되는 잡음원은 0 또는 1 중 한쪽으로 편향된 출력값이 생성될 가능성 존재
    이를 감소시키거나 없애기 위한 기법 - 해시함수를 이용(MD5, SHA-1 등)
    운영체제는 난수를 생성하는 내장형 메커니즘 제공
    리눅스는 4개의 엔트로피 소스(키보드, 마우스, 디스크 I/O 연산, 특정 인터럽트)를 사용하여 버퍼에 입력/저장, 이 중 일정 개수를 읽어 SHA-1 해시 함수를 통해 연산 진행

PRNG, 제대로 이해하기

Random Number?

난수는 예측 불가능성 을 만족하기 위해 무작위하게 생성되는 값을 말합니다. 이름에서 알 수 있듯이 정말 랜덤한 값을 뜻하죠.

암호학에서 난수를 굉장히 중요한 요소입니다.
아래와 같은 상황에서 사용하곤 합니다.

  1. 대칭키 자체, 공개키 암호에서의 개인키
  2. 블록암호 운용모드 - 초기화 벡터(IV), 카운터(CTR) 생성
  3. 패스워드 기반 암호 - 솔트 (Salt) 생성

그런데, 사용되는 난수들은 정말 랜덤할까요?

난수의 성질

  • 무작위성 Randomness: 통계적인 편중이 없이 수열이 무작위로 되어 있는 성질로 ‘아무렇게’ 처럼 보이는 성질
  • 예측 불가능성 Unpredictability: 과거의 의사난수열로부터 다음 생성될 수를 예측할 수 없는 성질
  • 재현 불가능성 Reconstruction is impossible: 같은 수열을 재혈할 수 없다는 성질

무작위성 Randomness

통계적인 성질을 조사했을 때, 치우침이 없으면 무작위하다고 판단합니다.
난수가 무작위성만 가진다면 안전할까요? 무작위하다고만 해서 예측할 수 없다는 건 불충분합니다.
무작위성만 가지는 난수 -> 약한 의사 난수 (Pseudo Random)

예측 불가능성 Unpredictability

공격자가 모든 의사난수열을 얻는다고 할지라도 다음에 출력될 난수를 예측할 수 없어야 합니다.

  • 아래에서 언급하겠지만, 의사난수 생성기(PRNG)의 Seed 또한 강한 의사난수입니다.
    일반적으로 PRNG에서 사용되는 알고리즘 자체는 공격자가 알고 있기 때문에 의사난수를 생성하기 위한 초기값이 되는 값(seed)는 알려져서는 안됩니다(예측 불가능해야 함). 예측 불가능성을 가지는 난수 -> 강한 의사 난수 (Pseudo Random)
    강한 의사난수는 당연히 무작위성을 가집니다.
    강한 의사난수를 가질 때부터 암호 기술에 사용할 수 있습니다.
    그래서 암호 시스템에 사용되기 위해서는 적어도 예측 불가능성을 가져야 합니다.

재현 불가능성 Reconstruction is impossible

진정한 난수를 이루는 조건이 아닌가 싶은데요.
재현 불가능성을 가지는 난수 -> 진성 난수 (True Random)

하지만, 컴퓨터의 특성상 규칙적으로 동일한 매커니즘을 갖기 때문에 한계가 있습니다.
그래서 재현불가능한 물리현상으로부터 정보를 얻을 수 있습니다.
예를 들어 당일의 온도나 습도, 소리와 변화 등, 사용자의 마우스 커서의 움직임, 키 스트록의 입력 변화 값 등이 있죠. 혹은 방사선 관측기의 출력도 있습니다.

Randomness ?

암호학에서 아주 중요한 역할이죠.
아무렇게나 보이는 성질입니다.

무작위성의 확률분포

아래의 엔트로피를 설명하기 전에 확률분포에 대해 알아보도록 합시다.
무작위 과정 Randomized Process의 모든 가능한 결과는 확률분포로 특정지어 집니다.
절대 일어나지 않는다는 의미인 0부터 반드시 일어난다는 1까지의 숫자로 표시됩니다.

확률분포는 모든 다능한 결과를 포함해야 하며, 반드시 모든 확률의 합이 1이어야 합니다.
확률분포는 균등분포와 비균등분포가 있습니다.

  • 균등 분포 uniform distribution: 모든 확률이 같은 확률분포.
  • 비균등 분포 non-uniform distribution: 모든 확률이 동일하지 않은 분포.

RNG

RNG는 Random Number Generator 로, 난수 생성기를 의미합니다.
그렇다면, 난수는 어떻게 생성할 수 있을까요?

난수를 만드는 경우에 대해 위에서 한 번 언급했는데요.
다시 정리하자면 다음과 같습니다.

  • 아날로그 정보를 사용하여 엔트로피를 수집
    ex) 온도, 습도, 소리 등의 데이터
    하지만 측정이 어려울 때가 많습니다.

  • 사용자의 활동을 통한 엔트로피 수집
    ex) 커서의 움직임, 키보드 키 스트록 시퀀스, 네트워크나 디스크 활동
    하지만 공격자로부터의 조작과 악용에 취약하다는 점이 있습니다.

  • 양자 난수 발생기
    이론적으로 True Random을 얻을 수 있지만, 빠르게 산출하지 못하는 기술적 어려움이 있습니다.

그래서 고안된 것이 짧은 진성 난수열을 통해 긴 난수열을 생성하는 방법입니다.
이것이 바로 의사난수발생기 Pseudo Random Number Generator 입니다.

참고로, 난수 발생기는 그림과 같이 존재합니다.

RNG

TRNG (진성난수발생기)를 통해 PRNG(의사난수발생기)의 Seed 값을 생성합니다.

PRNG

PRNG는 Pseudo Random Number Generator의 약자로, 의사 난수 발생기라고 합니다.

단어에서 느낄 수 있듯이 모방된 (가짜) 난수를 생성합니다.
완전한 Random 은 아니지만, Random 을 따라한 거죠.

PRNG 구성

PRNG
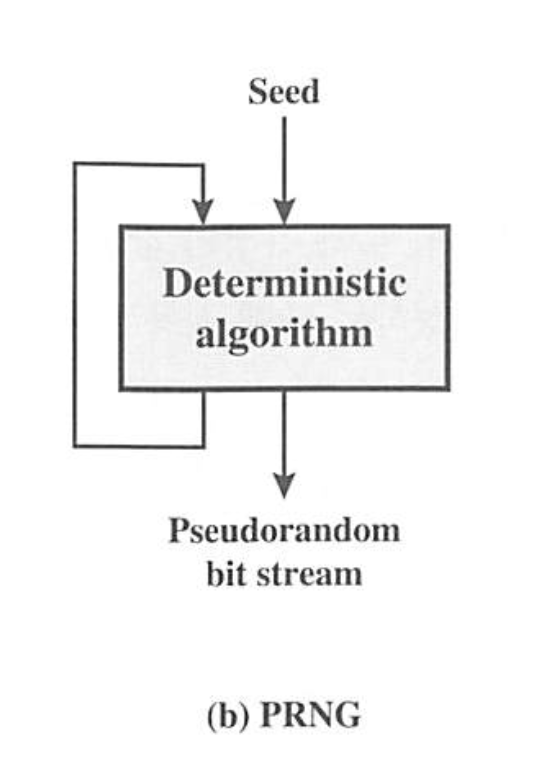
의사 난수 발생기를 도식화한 그림입니다.
짧은 진성난수인 Seed를 초기값으로 긴 의사난수열을 생성합니다.

  • Seed
    내부상태를 초기화하기 위해 사용되는 진성 난수 (Random한 비트열)이며, 외부에 알려져서는 안되며 예측가능하면 안되는 비밀 값입니다.

  • 내부 상태
    PRNG 가 관리하고 있는 메모리 값을 뜻합니다.
    이 값을 기초로 암호화하여 의사 난수를 도출시킵니다.
    이 값을 통해 의사난수가 발생하기 때문에 마찬가지로 외부에 알려져서는 안되며 예측가능해서는 안됩니다.

Seed 를 통해 내부 상태를 초기화하고 해시함수를 통해 의사 난수열을 생성합니다.
다음 의사난수열을 생성하기 위해 Seed 값을 1 증가시키기고 내부 상태를 업데이트합니다.
업데이트된 내부 상태를 통해 해시 함수를 통해 다음 의사 난수열을 생성합니다.

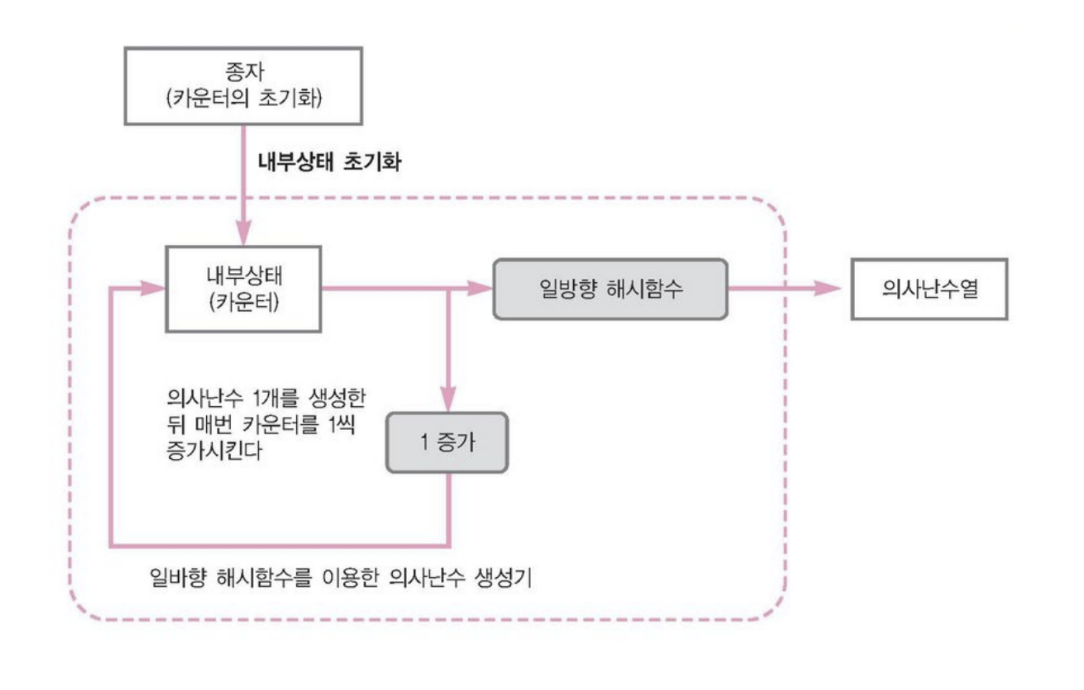
PRNG_2
일방향 해시 함수를 통해 예측 불가능성을 보장하고, 새로운 값을 도출시키기 위해 1을 증가하여 내부 상태를 업데이트 합니다.

이때, 해시함수를 거친 난수를 내부상태로 업데이트할 수 있을까요?
정답은 안됩니다.

ANSI X9.17 PRNG

ANSI

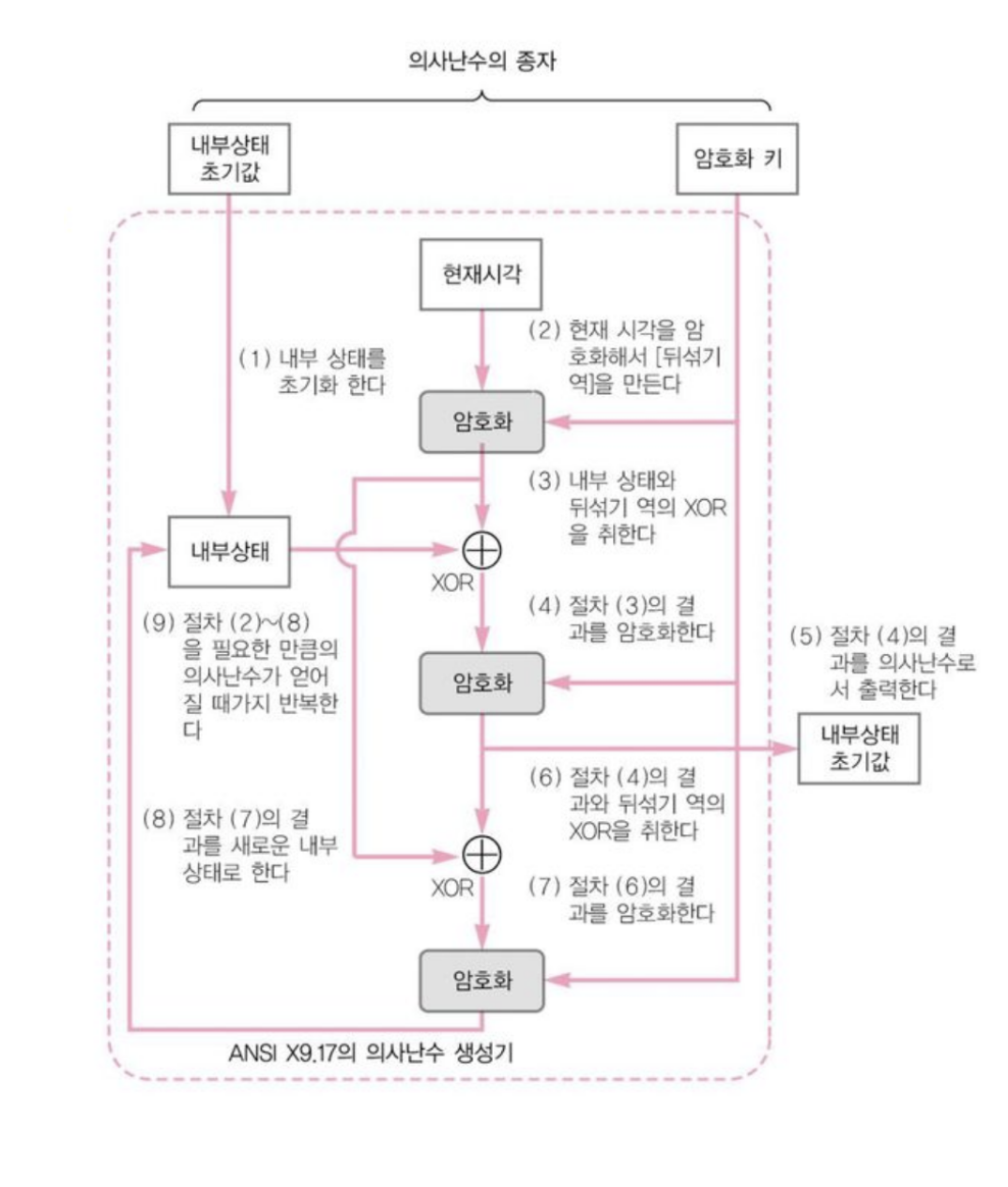
  1. Seed의 일부분을 내부상태를 초기화하고, 일부분을 암호화 키로 사용합니다.
  2. 현재 시각을 통해 암호화 키를 암호화 (A) 합니다.
  3. 초기화된 내부상태와 A를 XOR연산을 한 후 암호화 키와 함께 암호화(B) 합니다.
  4. B를 의사난수로 사용합니다. (그림에서 내부 상태 초기값으로 명시되어 있는데, 의사난수열입니다)
  5. B의 값을 A와 XOR한 후, 암호화 키를 이용해 암호화 (C) 합니다.
  6. C를 내부상태 값으로 Update 합니다.

그런데, 이 알고리즘을 사용하면 정말 안전할까요?
공격자는 발생기의 알고리즘을 알고 있고, 현재시각을 알 수 있습니다.
하지만 비밀값인 Seed를 통해 생성한 암호화키와 내부 상태 초기값을 알 수 없기 때문에
이 알고리즘은 내부 상태 값과 의사난수 값을 예측할 수 없기 때문에 안전하다고 할 수 있습니다.