2023.1.20.(금)
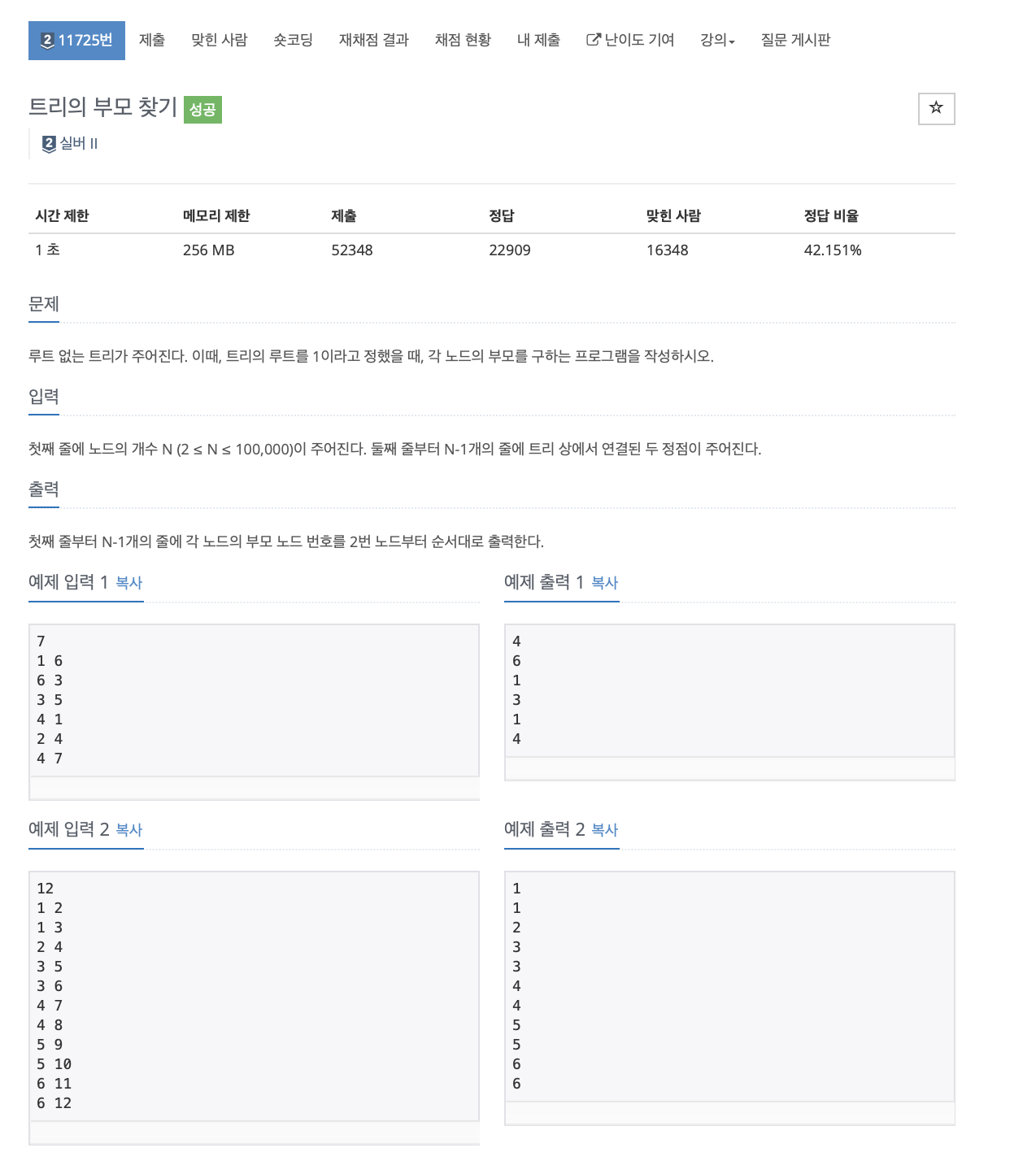
문제
접근 방법
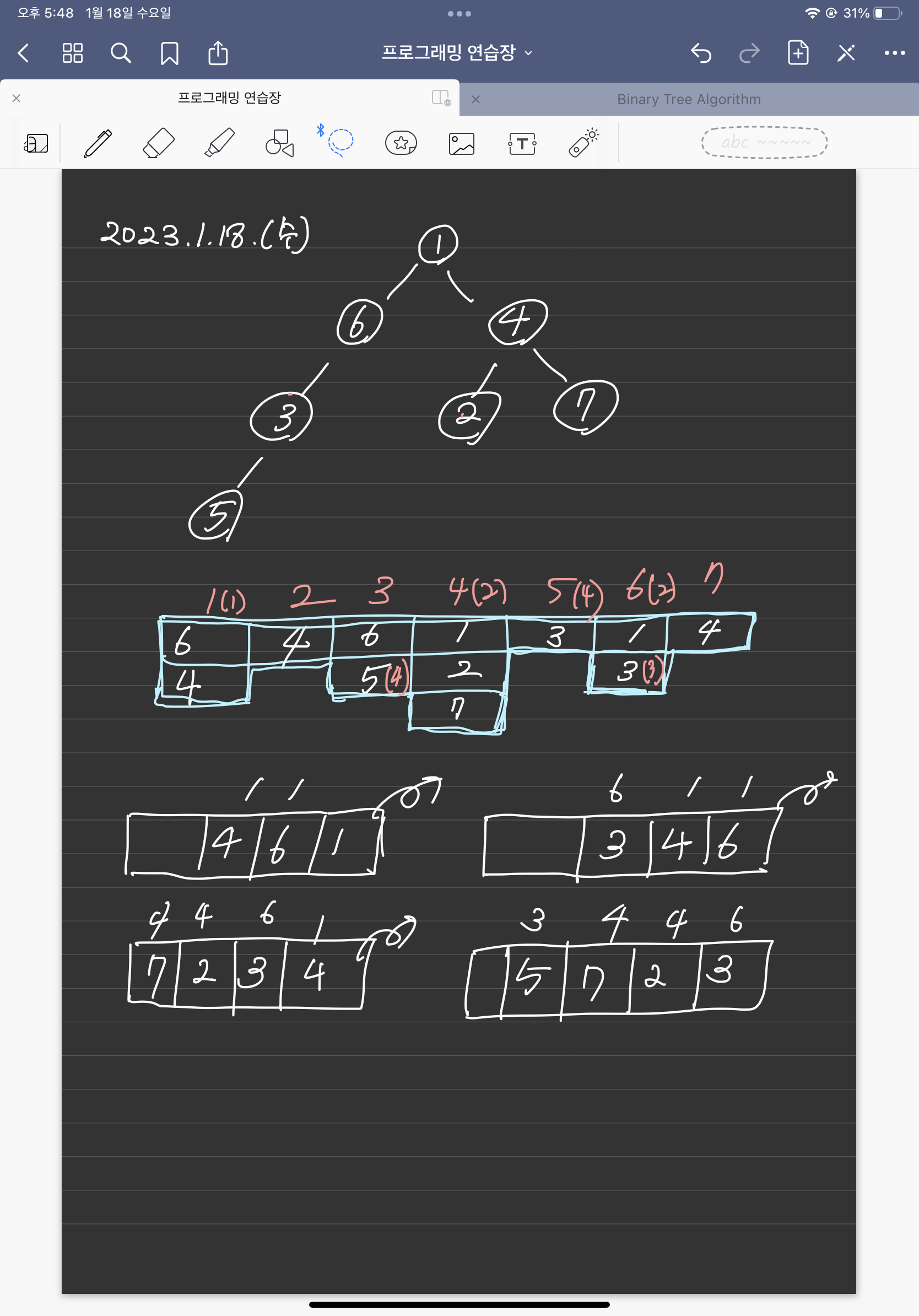
이 문제는 ‘트리’의 개념을 이해하고 있어야만 해결할 수 있습니다. 각 노드의 부모를 구하려면 어떻게 해야 할까요?
저는 먼저 벡터 배열 edges을 떠올렸습니다. 배열의 각 공간에 벡터가 들어가는 것이지요. 그림에서 파란색으로 그려낸 컨테이너가 바로 제가 표현하고자 하는 벡터 배열입니다. 노드의 개수가 최대 100,000개이니, 인덱스가 0부터 100,000까지인 벡터형 배열을 만듭니다. 만약에 입력값으로 1 6이 들어 온다면, 배열의 인덱스가 1인 곳에 6을 push_back() 하여, 1에 원소 6이 연결되었음을 표현합니다. 1의 입장에서 6이 연결된 것이라면, 6의 입장에서 또한 1과 연결된 것이겠죠. 따라서 인덱스가 6인 배열 공간의 벡터에 1을 push_back() 하여 넣어 줍니다.
우리에게는 컨테이너가 하나 더 필요합니다. 노드들의 연결을 나타내는 큐 que를 만들어 주어야 합니다. 그림을 보면 이해가 더 잘 될 텐데요, 그림의 벡터 배열에 집중해 주시기 바랍니다.
트리의 루트 노드는 항상 1이기 때문에 우리는 배열의 인덱스 1에서부터 시작을 할 겁니다. 따라서 큐에 먼저 1을 넣어두어야 하죠.
1에 연결된 노드들이 6과 4이기 때문에, 큐에 6과 4를 각각 푸쉬해 줍니다.
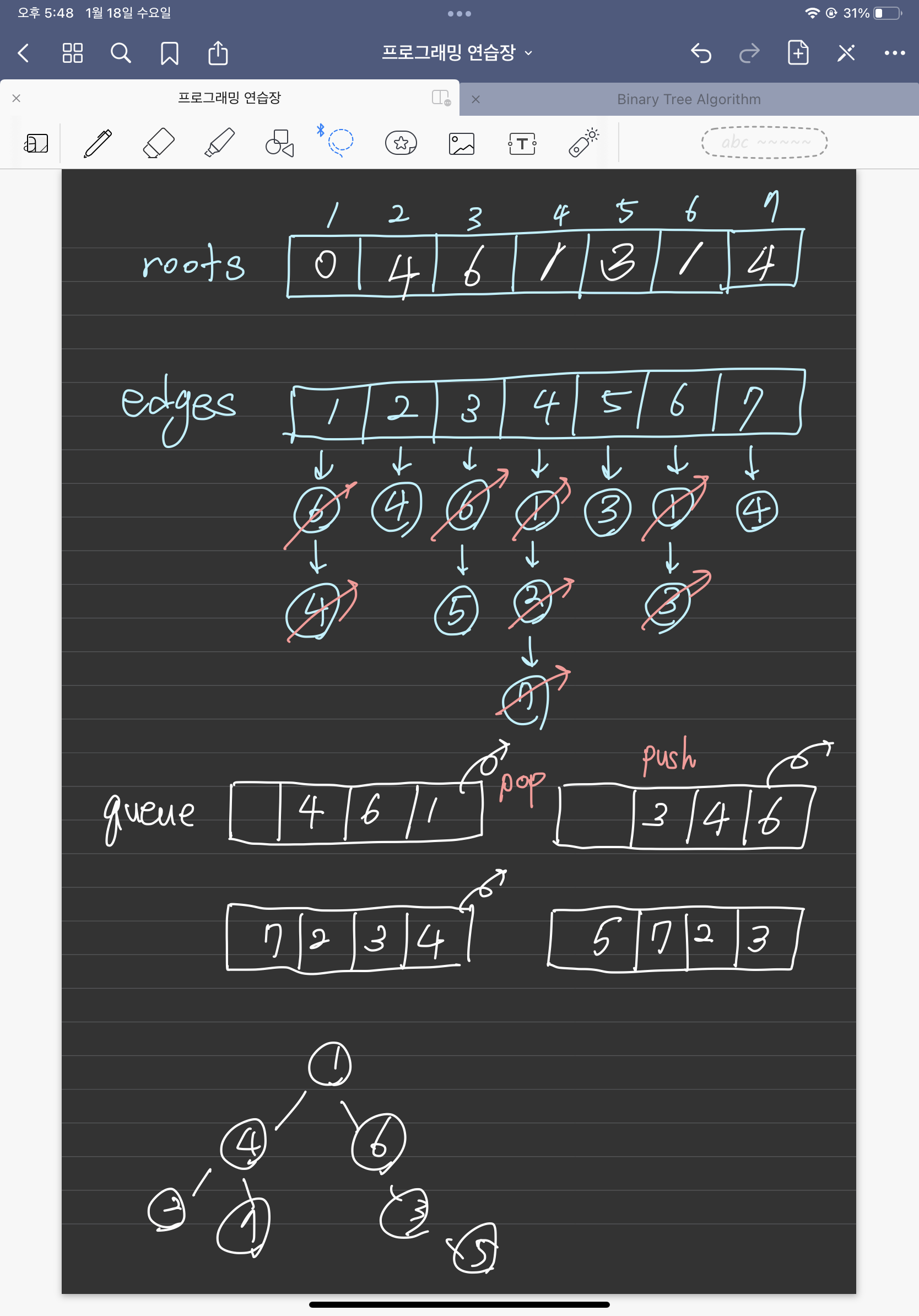
그리고 각 노드의 부모들을 기록해 둘 배열 roots도 만듭니다. 마찬가지로 크기가 100,001은 되어야겠죠.
큐에 6과 4를 넣는 과정에서, 여전히 큐의 front 값은 1이죠. 이 말은 즉슨, 6과 4의 부모가 1이라는 뜻입니다.
벡터 배열의 인덱스 1에 담겨 있는 숫자를 모두 넣을 때, 그 숫자들이 다시 인덱스가 되어 roots 배열 각 인덱스에 1이라는 숫자가 들어갑니다.
edges 벡터 배열 인덱스 1에 담겨 있는 모든 수를 큐에 넣었다면, 큐에서 1을 pop() 합니다. 그러면 큐의 front() 값은 이제 6이 되겠죠. 벡터 배열의 인덱스 6인 공간을 확인합니다. 1과 3이 들어 있군요.
1은 이미 방문하였으니 넘어가고 3은 큐에 넣습니다. roots의 인덱스 3에 큐의 front() 값인 6을 넣은 후에 6을 큐에서 뺍니다. 다시 front()는 4가 되고, 위 과정을 반복합니다.
이렇게 우리는 roots 배열의 인덱스에 해당하는 부모 노드를 모두 구하였습니다.
코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
vector<int> edges[100001];
queue<int> que;
int roots[100001] = {0};
int a, b;
for (int i = 1; i <= N-1; i++) {
cin >> a >> b;
edges[a].push_back(b);
edges[b].push_back(a);
}
que.push(1);
int pop;
while (!que.empty()) {
while (!edges[que.front()].empty()) {
pop = que.front();
que.push(edges[que.front()].back());
edges[que.front()].pop_back();
if (roots[que.back()] == 0) {
roots[que.back()] = pop;
}
}
que.pop();
}
for (int i = 2; i <= N; i++) {
cout << roots[i] << '\n';
}
}느낀점
<백준 9934번. 완전 이진 트리> 문제를 푸는 데에 실패하였습니다. 아무래도 제가 ‘중위 순회’나 ‘전위 순회’ 등과 같은 트리 순회를 어떻게 구현해야 하는지 잘 알지 못하기 때문인 것 같아요.
다른 이들의 코드를 보면 보통은 재귀함수로 구현이 되어있습니다. 하지만 아직도 저는 재귀적으로 사고하는 것이 잘 안됩니다. 얼마나 더 많은 데이터를 제 머릿속에 집어넣어야 익숙해 질까요?
재귀함수… 분할 정복… 언젠가는 이 둘을 정복하기를 바랍니다.